Programação Concorrente e Distribuída (3)
Esta página tem como objetivo apresentar a resolução dos exercícios do livro "An Introduction to Parallel Programming" de Peter Pacheco. A resolução dessas listas foi utilizada durante o curso de Programação Paralela no DCA / UFRN.
Respostas dos capítulos:
-
Chapter 03 - Distributed-Memory Programming with MPI
Chapter 03 - Distributed-Memory Programming with MPI
3.1. What happens in the greetings program if, instead of strlen(greeting)+1, we use strlen(greeting) for the length of the message being sent by processes 1, 2, ... , comm_sz - 1? What happens if we use MAX_STRING instead of strlen(greeting) + 1? Can you explain these results?
Quando é feita essa alteração, o resultado passa a ser:
 Esse erro acontece porque o caracter de terminação da string “\0”
não é enviado (por isso o motivo do strlen(greeting) + 1). Caso use o MAX_STRING, o
resultado é normal:
Esse erro acontece porque o caracter de terminação da string “\0”
não é enviado (por isso o motivo do strlen(greeting) + 1). Caso use o MAX_STRING, o
resultado é normal:

Apesar do processo que realiza o send preparar um buffer muito maior do que a mensagem que é efetivamente enviada, o processo 0 consegue receber com sucesso a mensagem que enviada pois o tamanho de recebimento também é MAX_STRING.
3.2. Modify the trapezoidal rule so that it will correctly estimate the integral even if comm_sz doesn’t evenly divide n. (You can still assume that n >= comm_sz.)
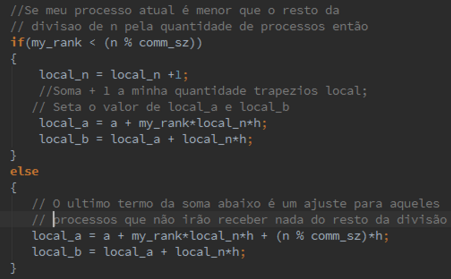
Para que o cálculo fique correto, alguns processos terão que aplicar a regra com um número maior de trapezoides quando o “comm_sz” não for divisível por “n”. O resto da divisão (n%p) deverá ser redristibuídos entre os processos começando pelo processo 0. E, além disso, os processos que não receberão os restos deverão ter seus ranges “afastados”. Segue a alteração que foi realizada:
3.3. Determine which of the variables in the trapezoidal rule program are local and which are global.

A variável “my_rank” é local, já que o valor dela é o índice do processo que está rodando no momento. Para cada processo, seu valor muda e é exclusivo. O “comm_sz” é global, já que seu valor é o mesmo para qualquer processo que o estiver executando, pois ela representa a quantidade de processos que estão executando no momento. O “n” é global, pois representa o número fixo de trapezoides que serão usados para calcular a integral com a regra do trapezoide. Cada processo terá o mesmo valor de “n”. O “local_n” é local, já que representa o número de trapezoides que cada processo irá receber e seu valor pode mudar para cada processo, dependendo do número de processos que estão executando e do processo que está usando essa variável. O “a” e o “b” são os limites fixos de integração utilizados por todos os processos, então elas são globais. O “h” também é global, já que representa o passo de integração usado por todos os processos. O “local_a” e o “local_b” são locais, já que representam os limites variáveis de integração para cada processo. Cada processo terá um “local_a” e um “local_b”. O “local_int” é local, já que representa o resultado local de cada processo de parte do cálculo da integração. O “total_int” é local, pois somente o processo 0 é responsável por calculá-lo (recebendo o local_int de todos os outros) e imprimi-lo.
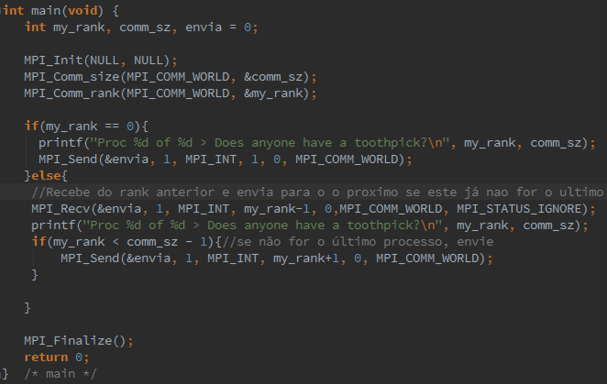
3.4. Modify the program that just prints a line of output from each process (mpi_output.c) so that the output is printed in process rank order: process 0s output first, then process 1s, and so on.
3.5. In a binary tree, there is a unique shortest path from each node to the root. The length of this path is often called the depth of the node. A binary tree in which every nonleaf has two children is called a full binary tree, and a full binary tree in which every leaf has the same depth is sometimes called a complete binary tree. See Figure 3.14. Use the principle of mathematical induction to prove that if T is a complete binary tree with n leaves, then the depth of the leaves is \(log_2(n)\).
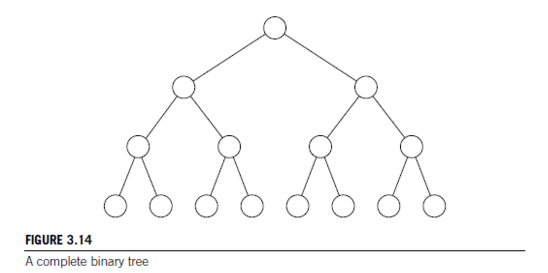
A profundidade de uma árvore é o caminho de comprimento mais curto entre uma raiz e uma folha em uma árvore. Para uma árvore binária T completa, seja n o número de folhas de T com profundidade limitada por P tem n = 2P. Com isso, temos que a profundidade P é igual a \(log_2(n)\). Provando isso por indução, temos que:
Passo base: Para \(n_0 = 2\), temos que \(P(2) = log_2(2) = 1\). A fórmula é verdadeira para \(n_0 = 2\).
2) Passo Indutivo: Se a fórmula é verdadeira para n = 2k, então deve ser verdadeira para \(n = 2^{k+1}\), ou seja, \( P( 2^k ) = P( 2^{k+1} ) \).
Supondo que a fórmula é verdadeira para n = 2k: $$ 2^k = 2^P = 2^{k+1} = 2^{P+1} $$
Com isso, podemos concluir que a afirmação é verdadeira.
3.6. Suppose comm_sz = 4 and suppose that x is a vector with n = 14 components. a. How would the components of x be distributed among the processes in a program that used a block distribution?
Em uma distribuição em bloco, o número n de elementos é dividido igualmente e em ordem entre os processos, caso o resultado da divisão entre n e comm_sz não tenha resto. Se tivermos resto, podemos distribui-lo em ordem entre os processos. Nessa questão, cada processo vai receber a divisão inteira de n/comm_sz = 14/4 = 3. O resto dessa divisão é 2, então os processos 0 e 1 vão receber 4 elementos cada e o resto irá receber 3. O resultado se encontra abaixo:
| Processos | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Elementos | x[0], x[1], x[2], x[12] | x[3], x[4], x[5], x[13] | x[6], x[7], x[8] | x[9], x[10], x[11] |
b. How would the components of x be distributed among the processes in a program that used a cyclic distribution?
Em uma distribuição cíclica, o número n de elementos é distribuído um por vez em cada processo em um determinado número de ciclos. O elemento x[0] vai para o processo 0, o x[1] vai para o processo 1, o x[2] vai para o processo 2 e o x[3] vai para o processo 3, fechando um ciclo. O próximo ciclo segue a mesma lógica. O resultado se encontra abaixo:
| Processos | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Elementos | x[0], x[1], x[8], x[12] | x[1], x[5], x[9], x[13] | x[2], x[6], x[10] | x[3], x[7], x[11] |
c. How would the components of x be distributed among the processes in a program that used a block-cyclic distribution with blocksize b = 2?
Em uma distribuição bloco-cíclica, há uma junção das propriedades de bloco e cíclica. Para um determinado b, o vetor x de n elementos seria dividido em blocos. O número de blocos seria n/b = 14/2 = 7. Caso a divisão inteira tivesse resto, ele seria distribuído entre os blocos seguindo sempre a mesma ordem. Segue um exemplo abaixo:
| Processos | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Elementos | x[0], x[1], x[8], x[9] | x[2], x[3], x[10], x[11] | x[4], x[5], x[12], x[13] | x[6], x[7] |
3.7. What do the various MPI collective functions do if the communicator contains a single process?
Se as funções coletivas do MPI tiverem apenas um processo em seu comunicador, não ocorre problemas no programa, já que a comunicação é dada por todos-para-um, um-para-todos ou todos-para-todos. Nesse caso em particular, “todos” seria o próprio processo. Toda a informação é enviada e recebida pelo mesmo processo.
3.8. Suppose comm_sz = 8 and n = 16.
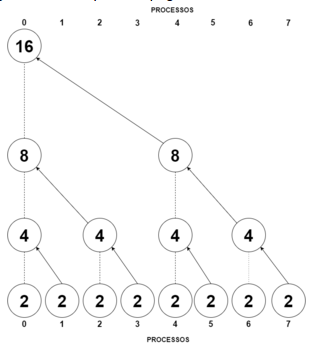
a. Draw a diagram that shows how MPI_Scatter can be implemented using tree-structured communication with comm_sz processes when process 0 needs to distribute an array containing n elements.
Os elementos do vetor são distribuídos para que todos fiquem com a quantidade de n/comm_sz = 16/8 = 2. O processo 0 divide pela metade o número de elementos e envia para o processo 4 e assim por diante com todos os processos até que todos tenham o mesmo número de elementos do vetor. Diagrama está na próxima página:
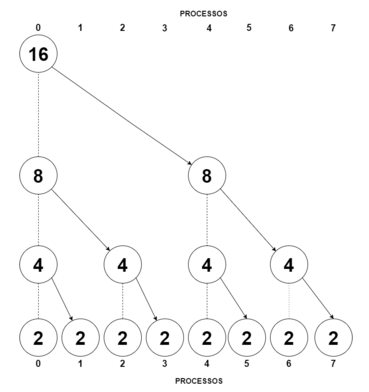
b. Draw a diagram that shows how MPI_Gather can be implemented using tree-structured communication when an n-element array that has been distributed among comm_sz processes needs to be gathered onto process 0.
Todos os processos tem que enviar seus elementos para o processo 0. O processo 1 envia seus elementos pro processo 0, o processo 3 envia seus elementos para o processo 2 e assim por diante. O diagrama está na próxima página:
3.9. Write an MPI program that implements multiplication of a vector by a scalar and dot product. The user should enter two vectors and a scalar, all of which are read in by process 0 and distributed among the processes. The results are calculated and collected onto process 0, which prints them. You can assume that n, the order of the vectors, is evenly divisible by comm_sz.
Código em anexo.
O princípio de funcionamento do programa é dado pela multiplicação do vetor1 pelo
escalar e o
produto desse resultado com o vetor2. O vetor1 e o vetor2 são divididos com o
MPI_Scatter entre os
processos e cada local_vetor1 e local_vetor2 são manipulados para depois terem seus
resultados
somados pelo MPI_Reduce. Exemplo de execução do código a seguir com 4 processos e
vetores de 4
elementos, lembrando que o tamanho dos vetores tem que ser divísivel pelo número de
processos:
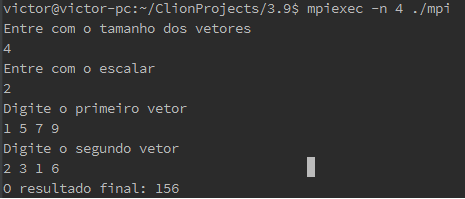
3.10 In the Read vector function shown in Program 3.9, we use local n as the actual argument for two of the formal arguments to MPI_Scatter : send count and recv count. Why is it OK to alias these arguments?
O vetor de dados referenciado por send_buf_p é dividido em local_n=n/comm_sz partes e cada parte é enviada para um processo. O parâmetro recv_count é a quantidade de elementos de send_buf_p que será recebida pelo processo 1. O parâmetro send_count é a quantidade de elementos enviada pelo processo 0 aos outros processos. Para a comunicação ser realizada com sucesso a quantidade de elementos enviados pelo processo 0 deve ser a mesma quantidade recebida pelos outros processos, portanto send_count e recv_count podem ter o mesmo nome ou nomes diferentes desde que tenham o mesmo valor.
3.11.
3.12.
3.13. MPI Scatter and MPI Gather have the limitation that each process must send or receive the same number of data items. When this is not the case, we must use the MPI functions MPI Gatherv and MPI Scatterv . Look at the man pages for these functions, and modify your vector sum, dot product pro- gram so that it can correctly handle the case when n isn’t evenly divisible by comm sz .
int geraSendCounts(int p, int n, int sendCounts[], int displs[]) {
int local_n = n / p;
int i;
for (i = 0; i < p; i++) {
if(i < (n % p))
{
sendCounts[i] = local_n +1;
displs[i] = i*(local_n + 1);
}
else
{
sendCounts[i] = local_n;
displs[i] = i*(local_n) + n % p;
}
}
}
if(my_rank < (n % comm_sz)) {
local_n = n / comm_sz + 1;
} else {
local_n = n / comm_sz;
}
//Aloca os vetores
vetor1 = (int*)malloc(n*sizeof(int));
vetor2 = (int*)malloc(n*sizeof(int));
local_vetor1 = (int*)malloc(local_n*sizeof(int));
local_vetor2 = (int*)malloc(local_n*sizeof(int));
int * sendCounts = (int*)malloc(comm_sz*sizeof(int));
int * displs = (int*)malloc(comm_sz*sizeof(int));
geraSendCounts(comm_sz, n, sendCounts, displs);
//Preenche os vetores e os distribui
if(my_rank == 0){
printf("Digite o primeiro vetor\n");
for(i=0;i<n;i++)
scanf("%d",&vetor1[i]);
printf("Digite o segundo vetor\n");
for(i=0;i<n;i++)
scanf("%d",&vetor2[i]);
}
MPI_Scatterv(vetor1, sendCounts, displs, MPI_INT,
local_vetor1, local_n, MPI_INT, 0, MPI_COMM_WORLD);
MPI_Scatterv(vetor2, sendCounts, displs, MPI_INT,
local_vetor2, local_n, MPI_INT, 0, MPI_COMM_WORLD);
3.14. a. Write a serial C program that defines a two-dimensional array in the main function. Just use numeric constants for the dimensions:
int two d[3][4];Initialize the array in the main function. After the array is initialized, call a function that attempts to print the array. The prototype for the function should look something like this.
void Print two d(int two d[][], int rows, int cols);After writing the function try to compile the program. Can you explain why it won’t compile?
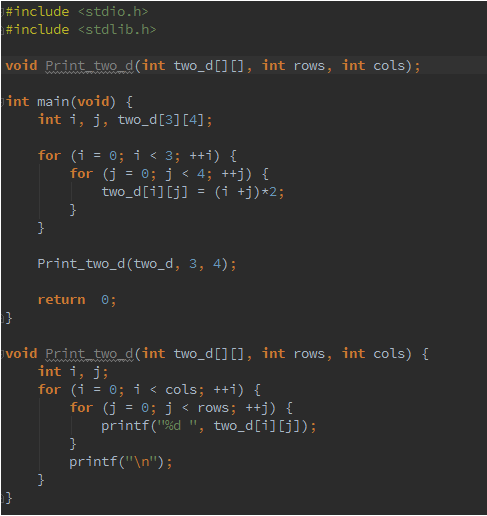
Uma matriz de 2 dimensões é um ponteiro de ponteiro. Ele não alocar memória sem saber a segunda dimensão da matriz.
b. After consulting a C reference (e.g., Kernighan and Ritchie [29]), modify the program so that it will compile and run, but so that it still uses a two-dimensional C array.

3.15. What is the relationship between the “row-major” storage for two-dimensional arrays that we discussed in Section 2.2.3 and the one-dimensional storage we use in Section 3.4.9?
Um array unidimensional é armazenado da linearmente na memória, com seus elementos posicionados um seguido do outro. O row-major é uma técnica de armazenar arrays multidimensionais em memórias lineares, como se representassem um grande vetor. Nessa técnica todos os elementos de uma linha são armazenados antes de se começar uma outra. Um elemento de um array bidimensional poderia ser facilmente acessado através de linha*tamanho + coluna.
3.16. Suppose comm sz = 8 and the vector x = (0, 1, 2, . . . , 15) has been distributed among the processes using a block distribution. Draw a diagram illustrating the steps in a butterfly implementation of allgather of x.
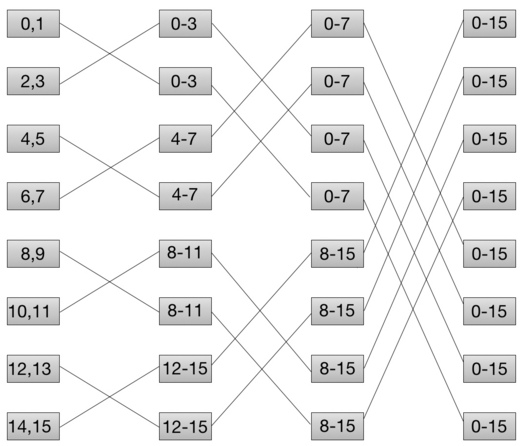
3.17. MPI Type contiguous can be used to build a derived datatype from a collection of contiguous elements in an array. Its syntax is
int MPI Type contiguous(
int count /∗ in ∗/,
MPI Datatype old_mpi_t /∗ in ∗/,
MPI Datatype∗ new mpi_t_p /∗ out ∗/);Modify the Read vector and Print vector functions so that they use an MPI datatype created by a call to MPI Type contiguous and a count argument of 1 in the calls to MPI Scatter and MPI Gather .
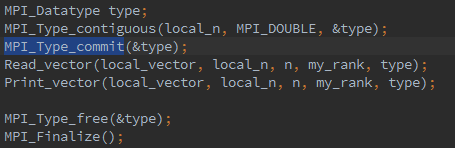
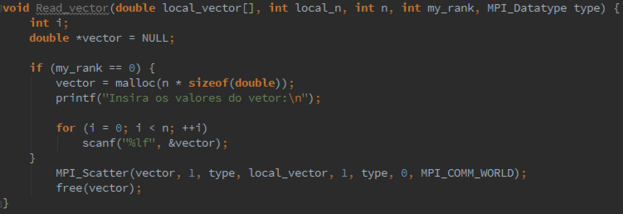
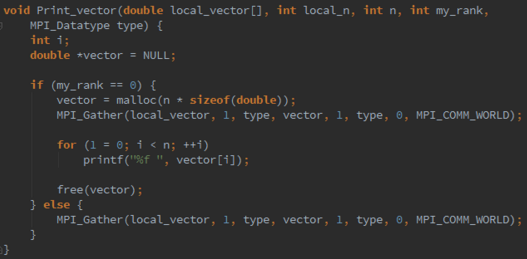
3.18. MPI Type vector can be used to build a derived datatype from a collection of blocks of elements in an array as long as the blocks all have the same size and they’re equally spaced. Its syntax is
int MPI Type vector(
int count /∗ in ∗/,
int blocklength /∗ in ∗/,
int stride /∗ in ∗/,
MPI Datatype old mpi t /∗ in ∗/,
MPI Datatype∗ new mpi t p /∗ out ∗/);
For example, if we had an array x of 18 doubles and we wanted to build a type corresponding to the elements in positions 0, 1, 6, 7, 12, 13, we could call
int MPI Type vector(3, 2, 6, MPI DOUBLE, &vect mpi t);since the type consists of 3 blocks, each of which has 2 elements, and the spacing between the starts of the blocks is 6 doubles. Write Read vector and Print vector functions that will allow process 0 to read and print, respectively, a vector with a block-cyclic distribution. But beware! Do not use MPI Scatter or MPI Gather . There is a technical issue involved in using these functions with types created with MPI Type vector . (See, for example, [23].) Just use a loop of sends on process 0 in Read vector and a loop of receives on process 0 in Print vector . The other processes should be able to complete their calls to Read vector and Print vector with a single call to MPI Recv and MPI Send . The communication on process 0 should use a derived datatype created by MPI Type vector . The calls on the other processes should just use the count argument to the communica- tion function, since they’re receiving/sending elements that they will store in contiguous array locations.
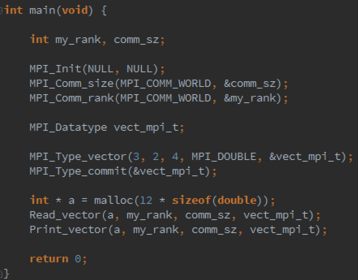
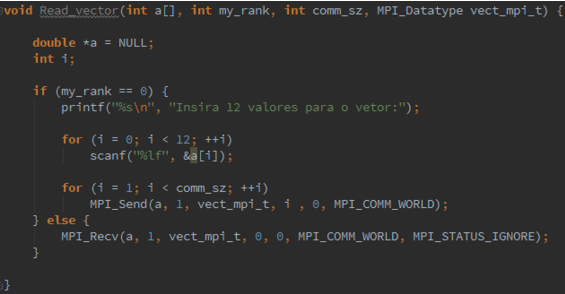
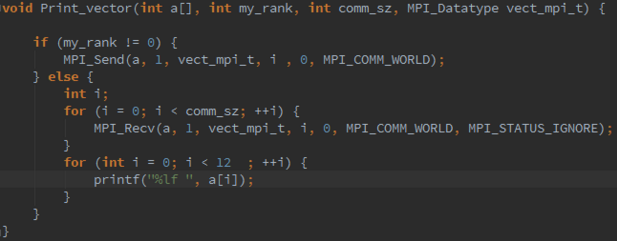
3.19. MPI_Type_indexed can be used to build a derived datatype from arbitrary array elements. Its syntax is
int MPI_Type_indexed(
int count /* in */,
int array_of_blocklengths[] /* in */,
int array_of_displacements[] /* in */,
MPI_Datatype old mpi_t /* in */,
MPI_Datatype new_mpi_t_p /* out */);
Unlike MPI_Type_create_struct, the displacements are measured in units of old mpi t—not bytes. Use MPI Type indexed to create a derived datatype that corresponds to the upper triangular part of a square matrix. For example, in the 4x4 matrix:
[ 0 1 2 3 ]
[ 4 5 6 7 ]
[ 8 9 10 11]
[12 13 14 15]
the upper triangular part is the elements 0, 1, 2, 3, 5, 6, 7, 10,11, 15. Process 0 should read in an nn matrix as a one-dimensional array, create the derived datatype, and send the upper triangular part with a single call to MPI Send. Process 1 should receive the upper triangular part with a single call to MPI Recv and then print the data it received.
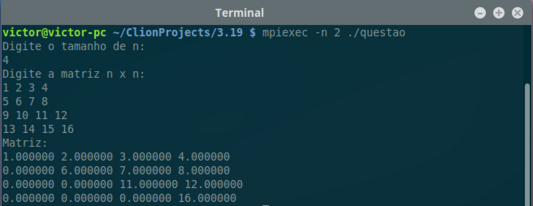

int main(void) {
int my_rank, comm_sz;
int n;
MPI_Comm mpi_comm = MPI_COMM_WORLD;
MPI_Init(NULL, NULL);
MPI_Comm_size(mpi_comm, &comm_sz);
MPI_Comm_rank(mpi_comm, &my_rank);
recebeN(&n, my_rank, mpi_comm);
double matriz[n*n];
MPI_Datatype novoTipo;
constroiTipoIndexado(matriz, n, &novoTipo);
if (my_rank == 0) {
lerMatriz(matriz, n);
MPI_Send(matriz, 1, novoTipo, 1, 0, mpi_comm);
} else {
MPI_Recv(matriz, 1, novoTipo, 0, 0, mpi_comm, MPI_STATUS_IGNORE);
imprimeMatrix(matriz, n);
}
MPI_Type_free(&novoTipo);
MPI_Finalize();
return 0;
}
void lerMatriz(double* matriz, int tamanho) {
printf("Digite a matriz n x n:\n");
int i;
for (i = 0; i < tamanho; i++) {
int j;
for (j = 0; j < tamanho; j++) {
scanf("%lf", &matriz[i*tamanho+j]);
}
}
}
void imprimeMatrix(double* matriz, int tamanho) {
printf("Matriz:\n");
int i;
for (i = 0; i < tamanho; i++) {
int j;
for (j = 0; j < tamanho; j++) {
printf("%f ", matriz[i*tamanho + j]);
}
printf("\n");
}
}
/**
* Constroi um tipo indexado do triangulo superior da matriz informada
* O tipo construído vem no seguinte formato:
*
* matriz = [ 0 1 2 ]
* [ 3 4 5 ]
* [ 6 7 8 ]
*
* novoTipoConstruido = ( [ 0 1 2 ],
* [ 4 5 ],
* [ 8 ] )
*
*/
void constroiTipoIndexado(double* matriz, int n, MPI_Datatype* novoTipoConstruido) {
int array_tamanhoDosBlocos[n];
int array_distancias[n];
array_distancias[0] = 0;
int i;
int j;
for (i = 0, j = n; i < n; i++, j--) {
// O tamanho dos arrays diminuem -1 a cada linha (triangulo superior)
array_tamanhoDosBlocos[i] = j;
}
for (i = 1; i < n; i++) {
//O deslocamento dele é o delslocamento do elementoAtual - o do primeiroElemento
array_distancias[i] = i*n + i;
}
MPI_Type_indexed(n, array_tamanhoDosBlocos, array_distancias, MPI_DOUBLE, novoTipoConstruido);
MPI_Type_commit(novoTipoConstruido);
}
void recebeN(int * n, int my_rank, MPI_Comm mpi_comm) {
if (my_rank == 0) {
printf("Digite o tamanho de n:\n");
scanf("%d", n);
MPI_Send(n, 1, MPI_INT, 1, 0, mpi_comm);
} else {
MPI_Recv(n, 1, MPI_INT, 0, 0, mpi_comm, MPI_STATUS_IGNORE);
}
}
3.20 The functions MPI Pack and MPI Unpack provide an alternative to derived datatypes for grouping data. MPI Pack copies the data to be sent, one block at a time, into a user-provided buffer. The buffer can then be sent and received. After the data is received, MPI Unpack can be used to unpack it from the receive buffer. The syntax of MPI Pack is:
int MPI Pack(
void∗ in buf /* in */,
int in buf count /* in */,
MPI Datatype datatype /* in */,
void∗ pack buf /* out */,
int pack buf sz /* in */,
int∗ position p /* in/out */,
MPI Comm comm /* in */);
We could therefore pack the input data to the trapezoidal rule program with the following code:
MPI Pack(&a, 1, MPI DOUBLE, pack buf, 100, &position, comm);
MPI Pack(&b, 1, MPI DOUBLE, pack buf, 100, &position, comm);
MPI Pack(&n, 1, MPI INT, pack buf, 100, &position, comm);
...
Write another Get input function for the trapezoidal rule program. This one should use MPI Pack on process 0 and MPI Unpack on the other processes.
/**
* Get input usando PACK e UNPACK
*/
void Get_input_pack(int my_rank, int comm_sz, double* a_p, double* b_p,
int* n_p) {
char pack_buf[1000];
if (my_rank == 0) {
int position = 0;
printf("Enter a, b, and n\n");
scanf("%lf %lf %d", a_p, b_p, n_p);
MPI_Pack(a_p, 1, MPI_DOUBLE, pack_buf, 1000, &position, MPI_COMM_WORLD);
MPI_Pack(b_p, 1, MPI_DOUBLE, pack_buf, 1000, &position, MPI_COMM_WORLD);
MPI_Pack(n_p, 1, MPI_INT, pack_buf, 1000, &position, MPI_COMM_WORLD);
}
int positionUnpack = 0;
MPI_Bcast(pack_buf, 1000, MPI_PACKED, 0, MPI_COMM_WORLD);
MPI_Unpack(pack_buf, 1000, &positionUnpack, a_p, 1, MPI_DOUBLE, MPI_COMM_WORLD);
MPI_Unpack(pack_buf, 1000, &positionUnpack, b_p, 1, MPI_DOUBLE, MPI_COMM_WORLD);
MPI_Unpack(pack_buf, 1000, &positionUnpack, n_p, 1, MPI_INT, MPI_COMM_WORLD);
}
3.21 How does your system compare to ours? What run-times does your system get for matrix-vector multiplication? What kind of variability do you see in the times for a given value of comm sz and n? Do the results tend to cluster around the minimum, the mean, or the median?
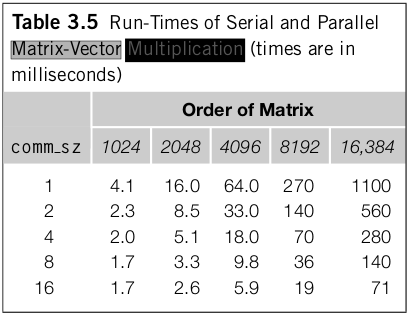
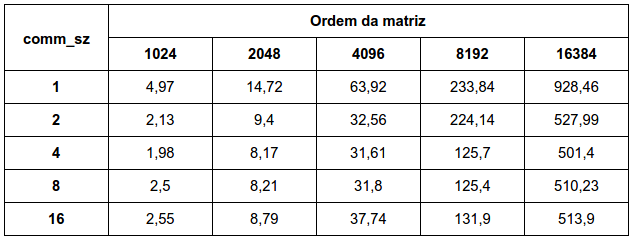
O algoritmo da multiplicação de matriz foi executado em um computador com quatro núcleos de processamento, assim a partir de comm_sz >= 4 praticamente não há diferença entre os valores para comm_sz maior ou igual a 4. Nota-se que o tempo de execução decai com o fator de crescimento de comm_sz. Assim se o comm_sz dobra, o tempo de execução tenderá a dobrar também. Pelas execuções que foram realizadas, pode-se concluir que o valor que melhor representa o resultado seria mediana, pois o resultado com a mediana fica mais robusto a possíveis tempos que estariam fora do padrão. Não poderia ser em torno do mínimo, pois a variação dos resultados normalmente é para um valor mediano Já em relação a média, seria sim, uma boa medida, no entanto ela é menos robusta a amostras fora do padrão do que a mediana.
3.22 Time our implementation of the trapezoidal rule that uses MPI Reduce. How will you choose n, the number of trapezoids? How do the minimum times compare to the mean and median times? What are the speedups? What are the efficiencies? On the basis of the data you collected, would you say that the trapezoidal rule is scalable?
MPI_Barrier(MPI_COMM_WORLD);
start = MPI_Wtime();
h = (b-a)/n; /* h is the same for all processes */
local_n = n/comm_sz; /* So is the number of trapezoids */
/* Length of each process' interval of
* integration = local_n*h. So my interval
* starts at: */
local_a = a + my_rank*local_n*h;
local_b = local_a + local_n*h;
local_int = Trap(local_a, local_b, local_n, h);
finish = MPI_Wtime();
loc_elapsed = finish-start;
MPI_Reduce(&loc_elapsed, &tempoMaximo, 1, MPI_DOUBLE, MPI_MAX, 0, MPI_COMM_WORLD);
MPI_Reduce(&loc_elapsed, &tempo_minimo, 1, MPI_DOUBLE, MPI_MIN, 0, MPI_COMM_WORLD);
MPI_Reduce(&loc_elapsed, &tempo_medio, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
/* Add up the integrals calculated by each process */
MPI_Reduce(&local_int, &total_int, 1, MPI_DOUBLE, MPI_SUM, 0,
MPI_COMM_WORLD);
/* Print the result */
if (my_rank == 0) {
printf("With n = %d trapezoids, our estimate\n", n);
printf("of the integral from %f to %f = %.15e\n",
a, b, total_int);
printf("Tempo Mínimo gasto = %e\n", tempo_minimo);
printf("Tempo Máximo gasto = %e\n", tempoMaximo);
printf("Tempo Médio gasto = %e\n", tempo_medio/comm_sz);
printf("Tempo Mediana gasto = %e\n", (tempoMaximo + tempo_minimo)/2.0);
}
$$ S = \frac{T_{serial}}{T_{parallel}}, E = \frac{S}{P} = \frac{\frac{T_{serial}}{T_{parallel}}}{p} = \frac{T_{serial}}{pT_{parallel}} $$
Executado para a = 0; b = 1000000; nTrapezios = 1000000:
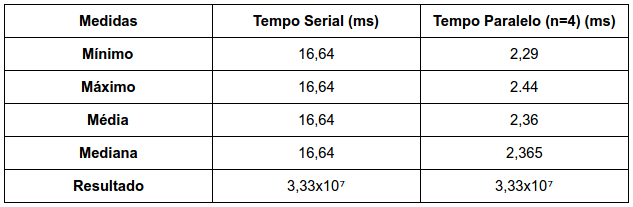
Resultados seriais para diferentes valores de nTrapézios: (de 0 a 1000000)
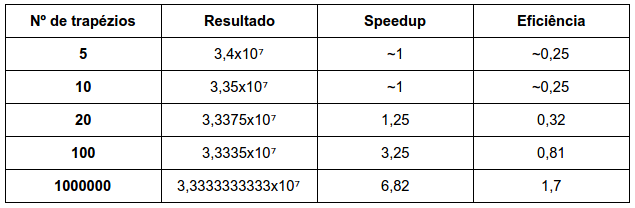
Teste de Escalabilidade:

O número de trapézios refletirá na precisão do resultado e no speedup e eficiência. Apesar do range de dados ser de 1milhão, não foi necessário um grande número de trapézios para se chegar a um valor adequado. Com 20 trapézios já foi possível ter um resultado com precisão de pelos menos duas casas decimais corretas. Com um maior número de trapézios o speed up e eficiência cresceram, o que indica que explorou mais a capacidade de execução em paralelo da aplicação. Portanto, o número de trapézios dependerá do quão preciso o usuário deseja que seja o seu resultado.
Nos resultados apresentados, o valor mínimo é bastante distante do valor médio, tratando-se sempre do melhor caso de execução. Possivelmente esta não é uma boa medida.
A regra do trapezoidal não é escalável pois duplicando o número de processadores e o tamanho do problema a eficiência não se manteve constante.
3.23. Although we don’t know the internals of the implementation of MPI Reduce, we might guess that it uses a structure similar to the binary tree we discussed. If this is the case, we would expect that its run-time would grow roughly at the rate of log 2 ( p), since there are roughly log 2 ( p) levels in the tree. (Here, p = comm sz .) Since the run-time of the serial trapezoidal rule is roughly pro- portional to n, the number of trapezoids, and the parallel trapezoidal rule simply applies the serial rule to n/p trapezoids on each process, with our assumption about MPI Reduce , we get a formula for the overall run-time of the parallel trapezoidal rule that looks like for some constants a and b.
a. Use the formula, the times you’ve taken in Exercise 3.22, and your favorite program for doing mathematical calculations (e.g., MATLAB ) to get a least-squares estimate of the values of a and b.
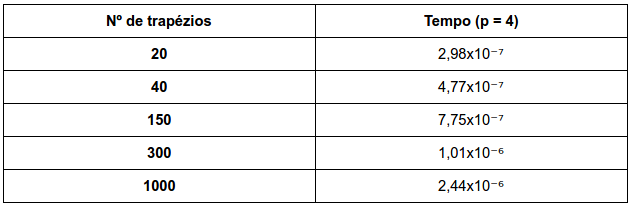
Usando a regra dos mínimos quadrados no Wolfram:
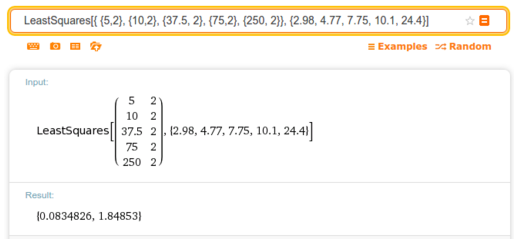
Primeira coluna da matriz M é n/p e a segunda coluna e log2(p), onde p sempre é 4. a = 0.08348x10⁻⁷ e b=1,84853x10⁻⁷
b. Comment on the quality of the predicted run-times using the formula and the values for a and b computed in part (a).
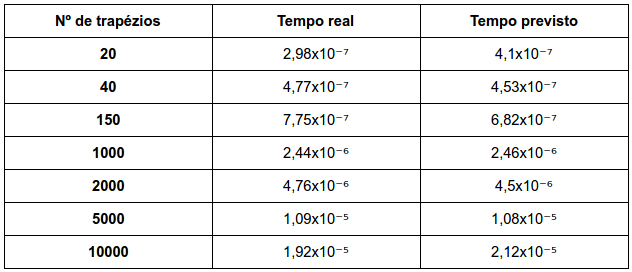
Os resultados previstos são satisfatórios e muito provável que é a implementação do MPI_REDUCE tenha sido em árvore binária como o livro supôs.
3.24. Take a look at Programming Assignment 3.7. The code that we outlined for timing the cost of sending messages should work even if the count argument is zero. What happens on your system when the count argument is 0? Can you explain why you get a nonzero elapsed time when you send a zero-byte message?
int main(void) {
int my_rank, comm_sz;
MPI_Comm mpi_comm = MPI_COMM_WORLD;
MPI_Init(NULL, NULL);
MPI_Comm_size(mpi_comm, &comm_sz);
MPI_Comm_rank(mpi_comm, &my_rank);
if (my_rank == 0) {
clock_t tempoInicial, tempoFinal;
int dadoEnviar = 5;
int dadoReceber;
tempoInicial = clock();
MPI_Send(&dadoEnviar, 1, MPI_INT, 1, 0, mpi_comm);
MPI_Recv(&dadoReceber, 1, MPI_INT, 1, 0, mpi_comm, MPI_STATUS_IGNORE);
tempoFinal = clock() - tempoInicial;
printf("Durou %f milissegundos\n", ((float)tempoFinal)*1000/CLOCKS_PER_SEC);
} else {
int dadoReceber;
int dadoEnviar = 3;
MPI_Recv(&dadoReceber, 1, MPI_INT, 0, 0, mpi_comm, MPI_STATUS_IGNORE);
MPI_Send(&dadoEnviar, 1, MPI_INT, 0, 0, mpi_comm);
}
MPI_Finalize();
return 0;
}
Com count = 0
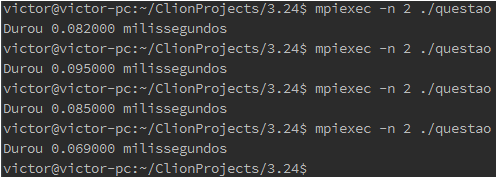
Com count = 1
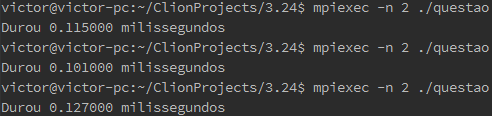
Com count=1 houve um pequeno overhead no envio da mensagem em comparação a count = 0. O que pode acontecer é que quando as funções MPI_SEND e MPI_RECV são invocadas, ambos processadores (remetente e destinatário) aguardam um ao outro chegarem nao mesmo momento de envio. Além disso o MPI pode ainda estar enviando uma mensagem vazia para o receptor. Isto pode ser a causa de ter obtido o tempo não nulo.
3.25. If comm_sz = p, we mentioned that the “ideal” speedup is p. Is it possible to do better?
$$ S = \frac{T_{serial}}{T_{parallel}} $$
O speedup “ideal” é p pois se dividíssemos o tempo serial igualmente para cada processador, teríamos um speedup de p vezes mais rápido, ou seja este seria uma espécia de speedup máximo na teoria. No entanto, na prática, é possível sim, ter um speedup maior do que p, chamado de Super-Linear SpeedUp. Isso acontece principalmente em computadores modernos que possuem implementações de cache, fazendo com que o speedup aumente mais do que p.
a. Consider a parallel program that computes a vector sum. If we only time the vector sum—that is, we ignore input and output of the vectors—how might this program achieve speedup greater than p?
Para p=1 se tivéssemos vários cache miss, o processador perderia um maior tempo para poder executar a soma de vetores. Para p > 1 e considerando que não teríamos cache miss em cada um dos processadores, teríamos um speed up maior do que p.
b. A program that achieves speedup greater than p is said to have super-linear speedup. Our vector sum example only achieved superlinear speedup by overcoming certain “resource limitations.” What were these resource limitations? Is it possible for a program to obtain superlinear speedup without overcoming resource limitations?
O exemplo da soma vetorial irá atingir um superlinear speedup se tivéssemos poucos ou nenhum cache miss, em relação a execução serial. No caso de um único processador executando a tarefa, pode acontecer que ele não consiga “cachear” todo o vetor em sua memória cache, tendo que acessar mais de uma vez a memória. Com vários processadores, cada um seria responsável pela soma de uma parte do vetor, sendo possível cachear totalmente ou parcialmente o seu vetor de soma na cache. Sem superar essas limitações de recurso não é possível obter um speedup superlinear.
3.26. Serial odd-even transposition sort of an n-element list can sort the list in considerably fewer than n phases. As an extreme example, if the input list is already sorted, the algorithm requires 0 phases.
a. Write a serial Is_sorted function that determines whether a list is sorted.
/**
* Verifica se o vetor 'a' está ordendo
* @return 1 se verdadeiro, 0 caso contrário
*/
int isSorted(int* a, int n) {
int isOrdenada = 1;
if (n > 0) {
int anterior = a[0];
for (int i = 1; i < n; i++) {
if (a[i] < anterior) {
isOrdenada = 0;
break;
}
}
}
return isOrdenada;
}
b. Modify the serial odd-even transposition sort program so that it checks whether the list is sorted after each phase.
/*-----------------------------------------------------------------
* Function: Odd_even_sort
* Purpose: Sort list using odd-even transposition sort
* In args: n
* In/out args: a
*/
void Odd_even_sort(
int a[] /* in/out */,
int n /* in */) {
int phase, i, temp;
for (phase = 0; phase < n; phase++) {
if (phase % 2 == 0) { /* Even phase */
for (i = 1; i < n; i += 2)
if (a[i - 1] > a[i]) {
temp = a[i];
a[i] = a[i - 1];
a[i - 1] = temp;
}
} else { /* Odd phase */
for (i = 1; i < n - 1; i += 2)
if (a[i] > a[i + 1]) {
temp = a[i];
a[i] = a[i + 1];
a[i + 1] = temp;
}
}
if (isSorted(a, n))
break;
}
} /* Odd_even_sort */
OBS: Melhor seria se a checagem fosse no início do for. No código acima, a checagem foi colocada no final do método porque a questão diz: ‘after each phase’
c. If this program is tested on a random collection of n-element lists, roughly what fraction get improved performance by checking whether the list is sorted?
No pior dos casos, se a lista já estivesse ordenada e a checagem não fosse feita o programa executaria as n fases. Com a checagem, o programa executaria apenas 1 fase (executaria nenhuma se a checagem fosse feita no início). Dificilmente uma lista aleatória já iria vir ordenada e a fração de melhoria com a adição de checagem seria de apenas uma situação dentro de n! outras.
3.27. Find the speedups and efficiencies of the parallel odd-even sort. Does the program obtain linear speedups? Is it scalable? Is it strongly scalable? Is it weakly scalable?
Tempo de Execução (x10⁻⁶ segundos):
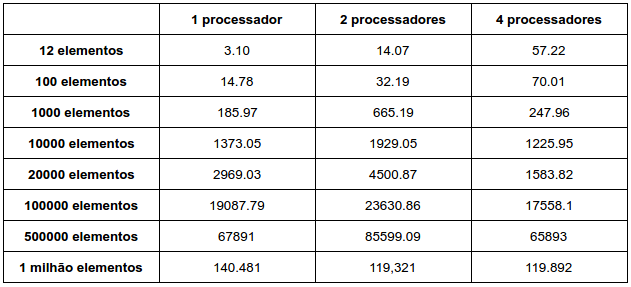

Como durante a execução do algoritmo é necessário a troca de mensagens entre os núcleos, o ganho não é tão notável quando se usa múltiplos processadores.
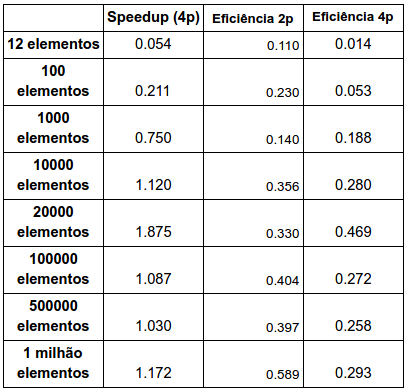
A speedup não linear pois ele não crescre linearmente com o tamanho do problema.
Teste de Escalabilidade:

Não é escalável pois a eficiência não se manteve constante. O programa mantém praticamente constante a eficiência enquanto aumenta o tamanho do problema e mantém-se o número de processadores, logo pode ser considerado como fracamente escalável. Não é fortemente escalável pois a eficiência não permanece constante com o aumento de processadores.