Programação Concorrente e Distribuída (2)
Esta página tem como objetivo apresentar a resolução dos exercícios do livro "An Introduction to Parallel Programming" de Peter Pacheco. A resolução dessas listas foi utilizada durante o curso de Programação Paralela no DCA / UFRN.
Respostas dos capítulos:
-
Chapter 02 - Parallel Hardware and Parallel Software
Chapter 02 - Parallel Hardware and Parallel Software
2.1 When we were discussing floating point addition, we made the simplifying assumption that each of the functional units took the same amount of time. Suppose that fetch and store each take 2 nanoseconds and the remaining operations each take 1 nanosecond.
a. How long does a floating point addition take with these assumptions?
As sete operações que são realizadas para a soma em ponto flutuante são: Buscar operandos, Comparar expoentes, Mover um operando, Adicionar, Normalizar o resultado, Arredondar o resultado, Armazenar o resultado. Supondo que as operações de busca e amazenamento demorem 2 nanosegundos e o resto das operações demore 1 nanosegundo, o total de tempo decorrido seria: 2+1+1+1+1+1+2 = 9 nanosegundos.
b. How long will an unpipelined addition of 1000 pairs of floats take with these assumptions?
Uma soma de 1000 float points feita normalmente e em sequência demoraria 1000 vezes o tempo de uma única soma: 9*1000=9000 nanosegundos.
c. How long will a pipelined addition of 1000 pairs of floats take with these assumptions?
Para a operação em pipeline sobre as operações da questão 2.1 a., são divididas em sete unidades funcionais. As unidades funcionam em sequência e a saída de uma unidade funcional é a entrada da próxima. Após realizar a primeira adição, que dura 9 nanosegundos, é produzido 1 resultado a cada 2 nanosegundos. Portanto o tempo total de execução do loop é de 2*999+9 = 2007 nanosegundos.
d. The time required for fetch and store may vary considerably if the operands/ results are stored in different levels of the memory hierarchy. Suppose that a fetch from a level 1 cache takes two nanoseconds, while a fetch from a level 2 cache takes five nanoseconds, and a fetch from main memory takes fifty nanoseconds. What happens to the pipeline when there is a level 1 cache miss on a fetch of one of the operands? What happens when there is a level 2 miss?
A ordem em que os dados são buscados na cache é do nível mais rápido ao mais lento.
Quando ocorre um level 1 cache miss:
Operação de busca = 2 nanosegundos para buscar na cache level 1 + 5 nanosegundos para buscar na cache
level 2 = 7 nanosegundos
Quando ocorre um level 2 cache miss:
Operação de busca = 2 nanosegundos para buscar na cache level 1 + 5 nanosegundos para buscar na cache
level 2 + 50 nanosegundos para buscar na memória principal = 57 nanosegundos.
2.2. Explain how a queue, implemented in hardware in the CPU, could be used to improve the performance of a write-through cache.
A fila fará com que as escritas mais recentes armazenadas na cache fiquem no topo. Isso facilita a escrita contínua a dados que são utilizados com mais frequência, melhorando o tráfego no barramento e sua utilização.
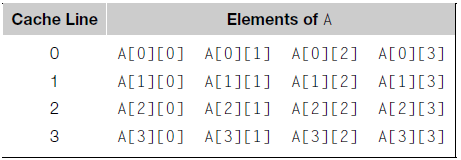
2.3. Recall the example involving cache reads of a two-dimensional array (page 22). How does a larger matrix and a larger cache affect the performance of the two pairs of nested loops? What happens if MAX = 8 and the cache can store four lines? How many misses occur in the reads of A in the first pair of nested loops? How many misses occur in the second pair?
Se apenas o tamanho da matriz for aumentado mais dados deverão ser carregados na cache pois provavelmente uma linha de cache não conseguirá mais armazenar uma linha inteira da matriz, resultando assim em uma execução mais lenta tanto do par de loops 1 quanto do par de loops 2. Se apenas o tamanho da cache for aumentado os loops executariam mais rápido devido à menor quantidade de cache miss (mais dados da matriz seriam carregados na cache). Porém a cache seria mais lenta, pois para cada cache miss uma quantidade maior de dados teria que ser carregada na cache.
Supondo MAX=8 e que a cache consegue armazenar 4 linhas com cada uma armazenando 4 elementos da matriz. O primeiro par de loops teria 16 cache misses, 2 para cada linha da matriz. O segundo par de loops teria 64 cache misses, pois mesmo com o aumento do número de linhas que a cache pode armazenar, o segundo par de loops ainda teria 1 cache miss para cada elemento lido da matriz.
2.4. In Table 2.2, virtual addresses consist of a byte offset of 12 bits and a virtual page number of 20 bits. How many pages can a program have if it’s run on a system with this page size and this virtual address size?
Se temos um espaço de endereços virtual de N bits (neste caso, N=32), e temos um tamanho de página de 2M (neste caso, M=12), então os primeiros N-M bits (neste caso, os primeiros 32-12 = 20 bits) compõem o número de páginas virtuais que que identificam unicamente cada página no espaço de endereços virtual. Os M bits nos dizem qual byte da página é o byte que está procurando, e é chamado de offset. Portanto o programa poderá ter até 220 = 1.048.576 páginas.
2.5. Does the addition of cache and virtual memory to a von Neumann system change its designation as an SISD system? What about the addition of pipelining? Multiple issue? Hardware multithreading?
Não. A adição de cache e memória virtual foram tentativas de superar o von Neumann bottleneck (gargalo), isto é, tentar evitar ao máximo o acesso a memória, visto que este acesso reduz a performance do sistema por ser mais custoso. Isto não muda sua característica de SISD.
Não. Pipelining pode ser claramente considerado hardware paralelo, já que unidades funcionais são replicadas. No entanto, esta forma de paralelismo não é comumente visível ao programador. De acordo com o livro-texto, hardware paralelo será limitado ao hardware que é visível ao programador, portanto pipelining é tratado como uma extensão do modelo básico de von Neumann.
Não. O mesmo conceito aplicado em pipelining também é aplicado em multiple issue.
Não. Hardware multithreading apenas providencia um meio para os sistemas continuarem executando trabalho útil quando uma task que está sendo executada for interrompida, por exemplo, se a task atual precisa esperar que dados sejam carregados da memória. Ao invés de procurar paralelismo na thread sendo executada, o sistema simplesmente carrega outra thread. Sistemas com hardware multithreading suportam switchings muito rápidos entre threads para que isso seja possível, mas isto não modifica a característica SISD do sistema.
2.6.
2.7. Discuss the differences in how a GPU and a vector processor might execute the following code:
Vector Processor: Caso o tamanho do array seja igual ao tamanho do vector processor todo esse loop será executado em um único ciclo de load, add e store. Caso o tamanho do array seja maior, serão necessários mais ciclos para executar todo este bloco.
GPU: A GPU funciona de forma similar ao vector processor. A principal diferença é o overhead que o sistema terá para enviar os dados para a GPU e depois para coletá-los.
2.8. Explain why the performance of a hardware multithreaded processing core might degrade if it had large caches and it ran many threads.
Múltiplas threads podem interferir umas nas outras quando compartilham recursos de hardware como caches ou translation lookaside buffers (TLB). Como resultado, tempos de execução de uma única thread não são melhorados mas degradados, mesmo quando apenas uma thread está executando, devido a baixas frequências ou estágios adicionais de pipelining que são necessários para acomodar thread-switching hardware.
2.9. In our discussion of parallel hardware, we used Flynn’s taxonomy to identify three types of parallel systems: SISD, SIMD, and MIMD. None of our systems were identified as multiple instruction, single data, or MISD. How would an MISD system work? Give an example.
MISD (multiple instruction, single dada) é um tipo de arquitetura de computação paralela onde muitas unidades funcionais realizam diferentes operações no mesmo dado. Não existem muitas instâncias dessa arquitetura, já que MIMD e SIMD são frequentemente mais apropriadas para técnicas comuns de computação paralela. Especificamente, elas permitem melhor escalabilidade e uso de recursos computacionais do que a MISD. No entanto, um exemplo proeminente de computação MISD são os computadores de controle de vôo Space Shuttle. Fonte: Wikipedia.
2.10. Suppose a program must execute 1012 instructions in order to solve a particular problem. Suppose further that a single processor system can solve the problem in 106 seconds (about 11.6 days). So, on average, the single processor system executes 106 or a million instructions per second. Now suppose that the program has been parallelized for execution on a distributed-memory system. Suppose also that if the parallel program uses p processors, each processor will execute \( \frac{10^{12}}{p}\) instructions and each processor must send \(10^9(p - 1)\) messages. Finally, suppose that there is no additional overhead in executing the parallel program. That is, the program will complete after each processor has executed all of its instructions and sent all of its messages, and there won’t be any delays due to things such as waiting for messages.
a. Suppose it takes \(10^{-9}\) seconds to send a message. How long will it take the program to run with 1000 processors, if each processor is as fast as the single processor on which the serial program was run?
Serão executadas \(\frac{10^{12}}{1000}\) instruções em cada processador, isso resulta em 109 por processador. Se eles estão em paralelo, então demorará 103 segundos para que as instruções sejam executadas, pois são 106 instruções por segundo. Também serão enviadas 109(1000-1) mensagens, resultando em 999 * 109 mensagens. Se demora 10-9 segundos pra enviar uma mensagem, então será 999 * 109 * 10-9. Isso resulta em 999 segundos. O resultado final será 999 + 103 = 1999 segundos.
b. Suppose it takes 10-3 seconds to send a message. How long will it take the program to run with 1000 processors?
Usando a mesma lógica da questão (a), isso resultará em 999 * 106 + 103 = 999001000 segundos, aproximadamente 11562,5 dias.
2.11. Derive formulas for the total number of links in the various distributed memory interconnects.
Em um sistema de memória distribuída, cada processador está emparelhado com sua própria memória privada, e os pares de processador-memória se comunicam através de uma rede interconectada. Nesses sistemas, os processadores geralmente se comunicam explicitamente ao enviar mensagens ou ao usar funções especiais que provem acesso à memória de outro processador. As interconexões de um sistema de memória distribuída são divididas em dois grupos: interconexões diretas e indiretas. Em uma interconexão direta, cada switch é diretamente conectado a um par processador-memória, e os switches são conectados entre si. Nossas formulas serão baseadas no número p de processadores para achar o número de conexões. Um tipo de interconexão direta é do tipo anel, há 2p conexões, já que um switch só pode se conectar a outros 2 switchs e 1 processador. Na malha toroidal, existem 3p conexões, já que um switch pode se conectar a outros 4 switches e 1 processador. A interconexão direta ideal é a completamente conectada, em que todos os switches estão conectados com todos os outros switches e 1 processador para cada, o número de conexões é dado por p2 / 2+p/2. Também existe o hipercubo. Ele é construído indiretamente. Um hipercubo de 1 dimensão é completamente conectado entre 2 switchs, um de 2 dimensões é a junção entre dois hipercubos de 1 dimensão ao conectar os switches correspondentes, assim por diante. Se existe um hipercubo de dimensão d, então p = 2d. O número de fios saindo de um switch é dado por \(1+d = 1 + log_2(p)\). Então o número de conexões entre os switches é dado por \(p *d/2 = (p * log_2(p))/2\). Em uma interconexão indireta, os switches podem não ser conectados diretamente a um processador. Eles são frequentemente montados com conexões unidirecionais e uma coleção de processadores, cada qual possui conexões de entrada e saída, e uma rede de comutação.
2.12.
2.13. a. Sketch a four-dimensional hypercube.
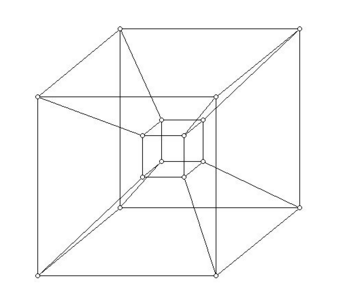
b. Use the inductive definition of a hypercube to explain why the bisection width of a hypercube is p/2.
A largura de bisseção do hipercubo é de p/2, já que essa interconexão sempre é formada pela junção de dois hipercubos de dimensão n-1, sendo n a dimensão do hipercubo que estamos analisando. Se cada hipercubo possui p’ nós e cada nó se conecta com outros p’ nós do outro hipercubo para formar o hipercubo atual, o número total de nós é p = 2p’, então a largura de bisseção vai ser o número de conexões entre os dois hipercubos, ou seja, metade do número total de nós. No exemplo acima, por exemplo, caso dividíssemos o hypercubo de 4 dimensões ao meio notaríamos que a bisceção seria 8, ou seja, metade do número de processadores.
2.14. To define the bisection width for indirect networks, the processors are partitioned into two groups so that each group has half the processors. Then, links are removed from anywhere in the network so that the two groups are no longer connected. The minimum number of links removed is the bisection width. When we count links, if the diagram uses unidirectional links, two unidirectional links count as one link. Show that an eight-by-eight crossbar has a bisection width less than or equal to eight. Also show that an omega network with eight processors has a bisection width less than or equal to four.
Em uma 8 por 8 crossbar, caso dividissemos ela ao meio notaremos que a o valor da bisceção será 4, ou seja, metade do número da dimensão da malha. No caso de um número ímpar, sempre teremos que remover algum link, para encontrar a bisceção, assim o seu valor semrpe será menor ou igual ao número da dimensão da malha. Já no caso da rede omega o tamanho da sua bisceção sempre será menor ou igual a metade do número de processadores. No caso de 8 processadores será necessárias apenas 4 redes para formar. Lembrando que uma rede com dois links uniderecionais são contados como uma única.
2.15. a. Suppose a shared-memory system uses snooping cache coherence and write-back caches. Also suppose that core 0 has the variable x in its cache, and it executes the assignment x = 5. Finally suppose that core 1 doesn’t have x in its cache, and after core 0’s update to x, core 1 tries to execute y = x. What value will be assigned to y? Why?
Na coerência de snooping cache, todos os núcleos do sistema de memória compartilhada são informados quando a linha de cache contendo alguma variável foi atualizada. Em write-back caches, o dado não é escrito imediatamente na memória. Em vez disso, o dado atualizado na cache é marcado como sujo, e quando a linha de cache é substituída por uma nova linha de cache da memória, a linha suja é escrita na memória. O novo valor de y vai ser 5, já que quando o núcleo 1 vai acessar a memória, a linha de cache suja pelo núcleo 0 é atualizada na memória.
b. Suppose that the shared-memory system in the previous part uses a directory-based protocol. What value will be assigned to y? Why?
No protocolo de cache baseada em diretório, existe uma estrutura de dados chamada de diretório. Ele armazena o status de cada linha de cache. Somente os núcleos usando determinada variável em suas memórias locais serão contatados. O valor de y será o que estava armazenado na memória, pois o núcleo 1 não estava utilizando a variável x.
c. Can you suggest how any problems you found in the first two parts might be solved?
Na primeira parte, o único problema que existe é que todos os núcleos são comunicados quando uma variável é modificada em uma linha de cache. E na segunda parte, somente os núcleos envolvidos são comunicados, isso pode gerar inconsistência, já que caso um outro núcleo queira acessar essa variável, ele só receberá o valor da memória e não o atualizado. Para resolver esses dois problemas, podemos criar uma tabela com o histórico das mudanças de status das variáveis que estão armazenadas na cache. Qualquer núcleo que fosse usar uma determinada variável, deve consultar essa tabela para saber se o valor dessa variável está suja. Se sim, deve atualizá-la na memória. Com isso, não é necessário que todos os núcleos sejam informados de mudanças em variáveis e não haverá inconsistências.
2.16. a. Suppose the run-time of a serial program is given by \(T_{serial} = n^2\), where the units of the run-time are in microseconds. Suppose that a parallelization of this program has run-time \(T_{parallel} = n2/p + log_2 p\). Write a program that finds the speedups and efficiencies of this program for various values of n and p. Run your program with n = 10, 20, 40, : : : , 320, and p = 1, 2, 4, : : : , 128. What happens to the speedups and efficiencies as p is increased and n is held fixed? What happens when p is fixed and n is increased?
/*Quantidade de valores que serão computados*/
float n = 10;
//Quantidade de núcleos do processador
float p = 1;
/*Tempo de execução serial em
microsegundos*/
float Tserial;
/*Tempo de execução paralela em
microsegundos*/
float Tparalelo;
for(int i=0;i<6;i++){
for(int j=0;j<8;j++){
Tserial = pow(n,2);
Tparalelo = pow(n,2)/p + log2(p);
cout << "O tempo de execucao serial sera " << Tserial << "us e o tempo de execucao paralela sera "<<Tparalelo<<"us para n = "<<n<<" e p = "<<p<<endl;
p*=2;
}
p=1;
n*=2;
}
Quando n é mantido fixo e p aumenta, o tempo de execução serial é mantido constante e o tempo de execução paralela decresce mais rapidamente quando o valor de n é maior que p. Quando p é mantido fixo e n aumenta, o tempo de execução serial cresce 4 vezes e o tempo de execução paralela cresce proporcionalmente a n.
b. Suppose that \(T_{parallel} = T_{serial}/p + T_{overhead}\) . Also suppose that we fix p and increase the problem size.
Show that if Toverhead grows more slowly than Tserial, the parallel efficiency will increase as we increase the problem size.
Se verificarmos a função da eficiência, no momento em que Toverhead cresce mais lentamente que o Tserial, a eficiência do tempo paralelo será praticamente modificado devido ao tempo serial que por sua vez cresce quadraticamente quanto maior o problema. Assim, o tempo paralelo estaria praticamente limitado ao tempo serial (já que p também seria fixo).
Show that if, on the other hand, Toverhead grows faster than Tserial, the parallel efficiency will decrease as we increase the problem size.
Neste caso, o tempo paralelo irá aumentar mais rápido quanto mais aumentamos o tempo serial. Com o valor de p fixo, a eficiência do tempo paralelo será reduzida.
$$ E = \frac{S}{P} = \frac{\frac{T_{serial}}{T_{paralelo}}}{p} $$
2.17.
2.18.
2.19. Suppose Tserial D n and Tparallel D n=pClog2.p/, where times are in microseconds. If we increase p by a factor of k, find a formula for how much we’ll need to increase n in order to maintain constant efficiency. How much should we increase n by if we double the number of processes from 8 to 16? Is the parallel program scalable?
$$ E(k'n,kp) = E(n,p) $$
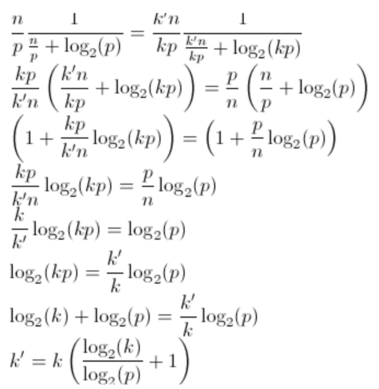
Para k=1 e p=8 temos k'=1. Aumentando o número de processos por um fator de 1 com k=2 e p=8 temos k'=2.6666… . Para um programa paralelo ser escalável temos que aumentar o tamanho do problema na mesma proporção que aumentamos a quantidade de processos. Para k=1 temos k'=1, mas quando aumentamos k por um fator de 1, k' aumenta por um fator de 1.6666… . Como não podemos aumentar o tamanho do problema na mesma taxa que aumentarmos a quantidade de processos, o programa paralelo não é escalável.
2.20. Is a program that obtains linear speedup strongly scalable? Explain your answer.
Sim. Se o programa tiver speedup linear significa que Tparalelo=Tserial/p. A definição do speedup de um programa paralelo é S=TserialTparalelo, então speedup linear tem S=p. Utilizando a definição de eficiência E=Sp=pp=1. Portanto a eficiência será sempre constante.
2.21. Bob has a program that he wants to time with two sets of data, input data1 and input data2. To get some idea of what to expect before adding timing functions to the code he’s interested in, he runs the program with two sets of data and the Unix shell command time:
$ time ./bobs prog < input data1
real 0m0.001s
user 0m0.001s
sys 0m0.000s
$ time ./bobs prog < input data2
real 1m1.234s
user 1m0.001s
sys 0m0.111s
The timer function Bob is using has millisecond resolution. Should Bob use it to time his program with the first set of data? What about the second set of data? Why or why not?
Ele não deveria usar com o primeiro conjunto de dados, já que a resolução precisa ser mais elevada, pois não dá para perceber o tempo que o programa demora para executar. Isso ocorre porque o programa executou rápido demais. Seria mais recomendável utilizar uma resolução de microsegundos. Já em relação ao segundo conjunto de dados, a resolução de milisegundos é satisfatória, pois dá para percebemos com mais precisão o tempo de execução do programa. Isso ocorre porque o programa executou um pouco mais lento.
2.22. As we saw in the preceding problem, the Unix shell command time reports the user time, the system time, and the “real” time or total elapsed time. Suppose that Bob has defined the following functions that can be called in a C program:
double utime(void);
double stime(void);
double rtime(void);
The first returns the number of seconds of user time that have elapsed since the program started execution, the second returns the number of system seconds, and the third returns the total number of seconds. Roughly, user time is time spent in the user code and library functions that don’t need to use the operating system—for example, sin and cos. System time is time spent in functions that do need to use the operating system—for example, printf and scanf.a. What is the mathematical relation among the three function values? That is, suppose the program contains the following code:
u = double utime(void);
s = double stime(void);
r = double rtime(void);
Write a formula that expresses the relation between u, s, and r. (You can assume that the time it takes to call the functions is negligible.)
Podemos perceber que o tempo total “r” é o tempo de executar as funções do programa
mais o tempo de execução de funções do sistema operacional. A relação se dá como abaixo:
r = u + s
b. On Bob’s system, any time that an MPI process spends waiting for messages isn’t counted by either utime or stime, but the time is counted by rtime. Explain how Bob can use these facts to determine whether an MPI process is spending too much time waiting for messages.
Ele pode definir que “e” é o tempo de espera do programa por mensagens do sistema operacional.
Ele pode usar a fórmula abaixo:
e = r – u – s
c. Bob has given Sally his timing functions. However, Sally has discovered that on her system, the time an MPI process spends waiting for messages is counted as user time. Furthermore, sending messages doesn’t use any system time. Can Sally use Bob’s functions to determine whether an MPI process is spending too much time waiting for messages? Explain your answer.
Sally não pode usar as funções de Bob para determina o tempo de espera por mensagens, já que ele já está embutido na função utime.
2.23. In our application of Foster’s methodology to the construction of a histogram, we essentially identified aggregate tasks with elements of data. An apparent alternative would be to identify aggregate tasks with elements of bin counts, so an aggregate task would consist of all increments of bin counts[b] and consequently all calls to Find bin that return b. Explain why this aggregation might be a problem.
A alternativa apresentada propõe que as tarefas fossem divididas por cada contagem de bin. Assim, por exemplo, uma dada tarefa seria responsável por realizar a contagem dos elementos que pertenceriam aos bin’s nas posições 0 e 1 e outra dos bin’s nas posições 2 e 3. Os problemas dessa proposta seriam que cada tarefa deveria realizar a chamada da função Find_bin para poder determinar se o elemento informado pertence ao bin que aquela tarefa é responsável por calcular. Isso é um problema, pois as tarefas estariam perdendo tempo na situação em que a tarefa identificasse que o elemento informado não pertence ao bin que ela é responsável. Um outro problema desta proposta é que quanto maior for o número de elementos no array de data[] maior será o tempo perdido por cada tarefa.
2.24. If you haven’t already done so in Chapter 1, try to write pseudo-code for our tree-structured global sum, which sums the elements of loc bin cts. First consider how this might be done in a shared-memory setting. Then consider how this might be done in a distributed-memory setting. In the shared-memory setting, which variables are shared and which are private?
Numa configuração de memória compartilhada, as tarefas deveriam solicitar o lock do bin_counts antes que realizassem o incremento. Nessa situação, portanto, o array de bin_counts seria uma variável compartilhada entre as tarefas, além do array de elementos. A variável privada proderia ser um array de local_bin_count, que armazenaria a seu próprio resultado. Na segunda etapa do processo, a tarefa solicitaria o lock do bin_counts e somaria os dois arrays. Pseudo-código a seguir:
bin_count[];
data[];
void tarefa() {
my_first_i = ....;
my_last_i = ....;
local_bin_count[bin_count.size];
for ( i = my_first_i; i < my_last_i; i++) {
int b = Find_Bin(data[i]);
local_bin_count[b]++;
}
lock ( bin_count ) {
// Soma local_bin_count com bin_count
}
}
Numa situação de memória distribuída, cada tarefa teria a sua local_bin_counts (variável privada) e não compartilhariam a soma do bin_counts total. A única variável compartilhada nessa situação seria o array de data[]. Cada tarefa estaria preocupada somente em resolver o seu intervalo de elementos e receber ou enviar seu somatório para outros realizarem a soma. Um possível pseudo-código seria:
data[];
void tarefa(sizeBinCount) {
my_first_i = ....;
my_last_i = ....;
local_bin_count[sizeBinCount];
for ( i = my_first_i; i < my_last_i; i++) {
int b = Find_Bin(data[i]);
local_bin_count[b]++;
}
if (/* decide se vai enviar */) {
} else {
// Recebe de outra tarefa
// Soma local_bin_count com o array recebido e envia para o próximo
}
}