Programação Concorrente e Distribuída (5)
Esta página tem como objetivo apresentar a resolução dos exercícios do livro "An Introduction to Parallel Programming" de Peter Pacheco. A resolução dessas listas foi utilizada durante o curso de Programação Paralela no DCA / UFRN.
Respostas dos capítulos:
-
Chapter 05 - Shared-Memory Programming with OpenMP
Chapter 05 - Shared-Memory Programming with OpenMP
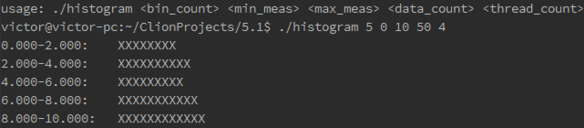
5.1 Use OpenMP to implement the parallel histogram program discussed in Chapter 2.
/*---------------------------------------------------------------------
* Function: Gen_bins
* Purpose: Compute max value for each bin, and store 0 as the
* number of values in each bin
* In args: min_meas: the minimum possible measurement
* max_meas: the maximum possible measurement
* bin_count: the number of bins
* Out args: bin_maxes: the maximum possible value for each bin
* bin_counts: the number of data values in each bin
*/
void Gen_bins(
float min_meas /* in */,
float max_meas /* in */,
float bin_maxes[] /* out */,
int bin_counts[] /* out */,
int bin_count /* in */) {
float bin_width;
int i;
bin_width = (max_meas - min_meas)/bin_count;
#pragma omp parallel for num_threads(thread_count) \
default(none) \
shared(min_meas, max_meas, bin_maxes, bin_counts, bin_count, bin_width) \
private(i)
for (i = 0; i < bin_count; i++) {
bin_maxes[i] = min_meas + (i+1)*bin_width;
bin_counts[i] = 0;
}
# ifdef DEBUG
printf("bin_maxes = ");
for (i = 0; i < bin_count; i++)
printf("%4.3f ", bin_maxes[i]);
printf("\n");
# endif
} /* Gen_bins */
/*---------------------------------------------------------------------
* Function: Gen_data
* Purpose: Generate random floats in the range min_meas <= x < max_meas
* In args: min_meas: the minimum possible value for the data
* max_meas: the maximum possible value for the data
* data_count: the number of measurements
* Out arg: data: the actual measurements
*/
void Gen_data(
float min_meas /* in */,
float max_meas /* in */,
float data[] /* out */,
int data_count /* in */) {
int i;
srandom(0);
#pragma omp parallel for num_threads(thread_count) \
default(none) shared(data, min_meas, max_meas, data_count)
for (i = 0; i < data_count; i++) {
data[i] = min_meas + (max_meas - min_meas) * random() / ((double) RAND_MAX);
}
# ifdef DEBUG
printf("data = ");
for (i = 0; i < data_count; i++)
printf("%4.3f ", data[i]);
printf("\n");
# endif
} /* Gen_data */
/* Count number of values in each bin */
#pragma omp parallel for num_threads(thread_count) default(none) \
shared(data_count, data, bin_maxes, bin_count, min_meas, bin_counts) \
private(bin, i)
for (i = 0; i < data_count; i++) {
bin = Which_bin(data[i], bin_maxes, bin_count, min_meas);
#pragma omp critical
bin_counts[bin]++;
}
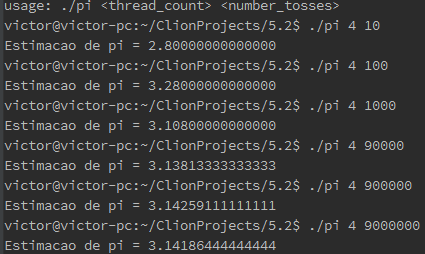
5.2. Suppose we toss darts randomly at a square dartboard, whose bullseye is at the origin, and whose sides are 2 feet in length. Suppose also that there’s a circle inscribed in the square dartboard. The radius of the circle is 1 foot, and it’s area is π square feet. If the points that are hit by the darts are uniformly distributed (and we always hit the square), then the number of darts that hit inside the circle should approximately satisfy the equation.
$$ \frac{number\ in\ circle}{total\ number\ of\ tosses} = \frac{\pi}{4} $$ since the ratio of the area of the circle to the area of the square is π/4. We can use this formula to estimate the value of π with a random number generator:number in circle = 0; for ( toss = 0; toss < number of tosses ; toss ++) { x = random double between − 1 and 1; y = random double between − 1 and 1; distance squared = x ∗ x + y ∗ y ; if ( distance squared <= 1) number in circle ++; } pi estimate = 4∗ number in circle /((double) number of tosses );This is called a “Monte Carlo” method, since it uses randomness (the dart tosses). Write an OpenMP program that uses a Monte Carlo method to estimate π. Read in the total number of tosses before forking any threads. Use a reduction clause to find the total number of darts hitting inside the circle. Print the result after joining all the threads. You may want to use long long int s for the number of hits in the circle and the number of tosses, since both may have to be very large to get a reasonable estimate of π.
int main(int argc, char* argv[]) {
long int number_tosses, number_in_circle;
int thread_count, i;
double x, y, distancia;
if (argc != 3) Usage(argv[0]);
thread_count = strtol(argv[1], NULL, 10);
number_tosses = strtoll(argv[2], NULL, 10);
if (thread_count < 1 || number_tosses < 1) Usage(argv[0]);
number_in_circle =0;
srandom(0);
# pragma omp parallel for num_threads(thread_count) \
reduction(+: number_in_circle) private(x, y, distancia)
for (i = 0; i < number_tosses; i++) {
x = num_aleatorio(); // Gera nnumero entre -1 e 1
y = num_aleatorio();
distancia = x*x + y*y;
if (distancia <= 1) {
number_in_circle += 1;
}
}
double pi = 4*number_in_circle/((double) number_tosses);
printf("Estimacao de pi = %.14f\n", pi);
return 0;
} /* main */
5.3. Count sort is a simple serial sorting algorithm that can be implemented as follows:
void Count sort (int a [], int n ) { int i , j , count ; int∗ temp = malloc ( n ∗sizeof(int)); for ( i = 0; i < n ; i ++) { count = 0; for ( j = 0; j < n ; j ++) if ( a [ j ] < a [ i ]) count ++; else if ( a [ j ] == a [ i ] && j < i ) count ++; temp [ count ] = a [ i ]; } memcpy ( a , temp , n ∗sizeof(int)); free ( temp ); } /∗ Count sort ∗/The basic idea is that for each element a[i] in the list a , we count the num- ber of elements in the list that are less than a[i] . Then we insert a[i] into a temporary list using the subscript determined by the count. There’s a slight problem with this approach when the list contains equal elements, since they could get assigned to the same slot in the temporary list. The code deals with this by incrementing the count for equal elements on the basis of the subscripts. If both a[i] == a[j] and j <i , then we count a[j] as being “less than” a[i] . After the algorithm has completed, we overwrite the original array with the temporary array using the string library function memcpy .
a. If we try to parallelize the for i loop (the outer loop), which variables should be private and which should be shared?
As variáveis a e n devem ser compartilhadas, já que seria necessário acessar a variável a e ter acesso ao seu tamanho. A variável temp também seria compartilhada, umas vez que cada posição do array só seria escrita por uma única thread. As variáveis i, j, count deveriam ser privadas.
b. If we parallelize the for i loop using the scoping you specified in the previous part, are there any loop-carried dependences? Explain your answer.
Não, não haveria nenhuma dependência entre as iterações uma vez que não seria necessário ter acesso a uma informação de uma outra iteração durante a execução do código. Além disso, a variável temp pode ser escrita pelas threads sem gerar problemas de concorrência.
c. Can we parallelize the call to memcpy ? Can we modify the code so that this part of the function will be parallelizable?
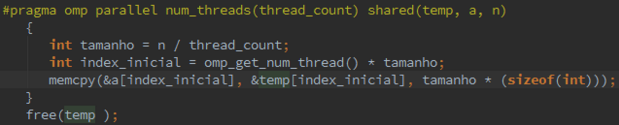
Sim, a chamada ao memcpy também poderia ser paralelizada. A única preocupação seria em relação ao tamanho de n que não deveria ser o mesmo. Além disso, o primeiro e o segundo argumento da função memcpy, deveria ser ponteiros para elementos do array a partir do qual deveria comecar a escrita. Segue o exemplo do código:
d. Write a C program that includes a parallel implementation of Count sort .
int main(int argc, char* argv[]) {
long int number_tosses, number_in_circle;
int thread_count, i, j, n, count;
srandom(0);
thread_count = strtol(argv[1], NULL, 10);
n = strtol(argv[2], NULL, 10);
int * a = malloc(n* sizeof(int));
geraMatriz(a, n);
//imprimeMatriz(a, n);
int * temp = malloc(n* sizeof(int));
double start = omp_get_wtime();
#pragma omp parallel for num_threads(thread_count) \
default(none) private(i, j, count) shared(a, n, temp, thread_count)
for (i = 0; i < n; i++) {
count = 0;
for (j = 0; j < n; j++)
if (a[j] < a[i])
count++;
else if (a[j] == a[i] && j < i)
count++;
temp[count] = a[i];
}
memcpy ( a , temp, n * sizeof(int));
double finish = omp_get_wtime();
free(temp );
printf("Tempo estimado %e segundos\n", finish - start);
//imprimeMatriz(a, n);
return 0;
} /* main */
e. How does the performance of your parallelization of Count sort compare to serial Count sort? How does it compare to the serial qsort library function?
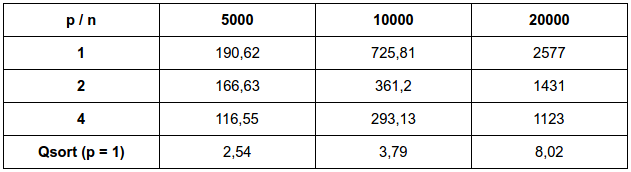
O quicksort possui complexidade de nlog(n) no melhor caso e no caso médio, e n² no pior caso, em comparação com o algoritmo n² do método count_sort apresentado.
5.4. Recall that when we solve a large linear system, we often use Gaussian elimination followed by backward substitution. Gaussian elimination converts an n × n linear system into an upper triangular linear system by using the “row operations.”
...
a. Determine whether the outer loop of the row-oriented algorithm can be parallelized.
O loop mais externo não é possível de ser paralelizado uma vez que existe dependências entre as iterações. O sistema é resolvido de baixo para cima (da última linha até a primeira) e o resultados das linhas mais abaixo são utilizadas para saber o resultado das linhas mais acima.
b. Determine whether the inner loop of the row-oriented algorithm can be parallelized.
O loop mais interno é capaz de ser paralelizado, no entanto, existe uma região crítica ao realizar o procedimento “x[row] -=” fazendo com que apenas uma thread realize a subtração por vez.
c. Determine whether the (second) outer loop of the column-oriented algorithm can be parallelized.
O loop mais externo não é possível de ser paralelizado pois existe dependência entre as iterações, pois os loops seguintes necessitam que seja executado a subtração realizada nos loops anteriores para poder proceder.
d. Determine whether the inner loop of the column-oriented algorithm can be parallelized.
O loop mais interno é possível sim de ser paralizado. Nesse caso não existe a região crítica como no caso do row-oriented.
e Write one OpenMP program for each of the loops that you determined could be parallelized. You may find the single directive useful—when a block of code is being executed in parallel and a sub-block should be executed by only one thread, the sub-block can be modified by a #pragma omp single directive. The threads in the executing team will block at the end of the directive until all of the threads have completed it.
Row Oriented:
Código Implementado - Row
Oriented
for (row = n - 1; row >= 0; row--) {
x[row] = b[row];
#pragma omp parallel for num_threads(thread_count) default(none) \
private(col) shared(x, b, a, n, row)
for (col = row + 1; col < n ; col++) {
double valor = a[row*n + col]*x[col];
#pragma omp critical
x[row] -= valor;
}
x[row] /= a[row*n + row];
}
Col Oriented:
Código Implementado - Col
Oriented
#pragma omp parallel for num_threads(thread_count) default(none) \
private(row) shared(x, b, n)
for (row = 0; row < n; row++) {
x[row] = b[row];
}
for (col = n -1; col >= 0; col--) {
x[col] /= a[col*n + col];
#pragma omp parallel for num_threads(thread_count) default(none) \
private(row) shared(x, b, a, n, col)
for (row = 0; row < col; row++) {
x[row] -= a[row*n + col]*x[col];
}
}
f. Modify your parallel loop with a schedule(runtime) clause and test the program with various schedules. If your upper triangular system has 10,000 variables, which schedule gives the best performance?

O que obteve melhor performance foi a execução default. O static obteve resultados próximos ao default, no entanto não conseguiu obter um resultado melhor. A pior execução foi o dynamic, pois ele adiciona overhead no sistema, pois os índices são definidos em tempo de execução. O guided obteve um bom resultado em relação ao dynamic, mas pior em relação ao static.
5.5.
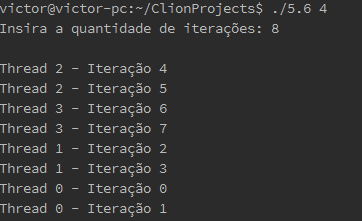
5.6 Write an OpenMP program that determines the default scheduling of parallel for loops. Its input should be the number of iterations, and its output should be which iterations of a parallelized for loop are executed by which thread. For example, if there are two threads and four iterations, the output might be:
Thread 0: Iterations 0 - 1
Thread 1: Iterations 2 - 3
int main(int argc, char *argv[]) {
long thread_count;
int i, iteracoes;
thread_count = strtol(argv[1], NULL, 10);
printf("Insira a quantidade de iterações: ");
scanf("%d", &iteracoes);
printf("\n");
# pragma omp parallel num_threads(thread_count)
# pragma omp for
for (i = 0; i < iteracoes; ++i) {
printf("Thread %d - Iteração %d\n", omp_get_thread_num(), i);
}
return 0;
}
5.7. In our first attempt to parallelize the program for estimating π, our program was incorrect. In fact, we used the result of the program when it was run with one thread as evidence that the program run with two threads was incorrect. Explain why we could “trust” the result of the program when it was run with one thread.
Quando o programa é executado com uma thread, a diretiva parallel não tem efeito, e o programa executa da mesma forma que o programa serial anterior. Assim, não há loop-carried dependence, já que existe apenas uma thread.
5.8. Consider the loop
a [0] = 0; for ( i = 1; i < n ; i ++) a [ i ] = a [ i − 1] + i ;There’s clearly a loop-carried dependence, as the value of a[i] can’t be com- puted without the value of a[i − 1]. Can you see a way to eliminate this dependence and parallelize the loop?
Fazendo o resultado de a[i] temos: a[0] = 0 a[1] = a[0] + 1 = 0 + 1 a[2] = a[1] + 2 = 0 + 1 + 2 a[3] = a[2] + 3 = 0 + 1 + 2 + 3 a[4] = a[3] + 4 = 0 + 1 + 2 + 3 + 4
O comportamento desse resultado pode ser representado pelo somatório:
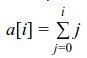
que é igual a:
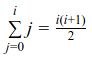
Logo o algoritmo se torna:
for (i = 0; i < n; i++) {
a[i] = i * (i + 1) / 2;
}
Neste loop o resultado de qualquer iteração não é usado novamente. Então o código pode ser paralelizado com a diretiva parallel for:
#pragma omp parallel for num_threads(thread_count) \
default(none) private(i) shared(a, n)
for (i = 0; i < n; i++) {
a[i] = i * (i + 1) / 2;
}
5.9. Modify the trapezoidal rule program that uses a parallel for directive ( omp trap 3.c ) so that the parallel for is modified by a schedule(runtime) clause. Run the program with various assignments to the environment variable OMP SCHEDULE and determine which iterations are assigned to which thread. This can be done by allocating an array iterations of n int s and in the Trap function assigning omp get thread num () to iterations [ i ] in the ith iteration of the for loop. What is the default assignment of iterations on your system? How are guided schedules determined?
No sistema utilizado se nenhuma clausula schedule for utilizada, o escalonamento padrão é aproximadamente uma partição em blocos. O sistema atribui um pouco mais de trabalho à thread 0 e um pouco menos à thread thread_count - 1.
/*------------------------------------------------------------------
* Function: Trap
* Purpose: Use trapezoidal rule to estimate definite integral
* Input args:
* a: left endpoint
* b: right endpoint
* n: number of trapezoids
* Return val:
* approx: estimate of integral from a to b of f(x)
*/
double Trap(double a, double b, int n, int thread_count, int *iterations) {
double h, approx;
int i;
h = (b-a)/n;
approx = (f(a) + f(b))/2.0;
# pragma omp parallel for num_threads(thread_count) \
reduction(+: approx) schedule(runtime)
for (i = 1; i <= n-1; i++) {
approx += f(a + i*h);
iterations[i-1] = omp_get_thread_num();
}
approx = h*approx;
return approx;
} /* Trap */

Se a clausula schedule é incluída e OMP_SCHEDULE é definida para guided, então aproximadamente n/thread_count iterações são atribuídas para uma thread, e sucessivos blocos de iterações consecutivas tem aproximadamente metade do tamanho do bloco anterior. Neste caso também a atribuição de iterações varia para cada execução.

5.10.
5.11. Recall that in C, a function that takes a two-dimensional array argument must specify the number of columns in the argument list, so it is quite common for C programmers to only use one-dimensional arrays, and to write explicit code for converting pairs of subscripts into a single dimension. Modify the OpenMP matrix-vector multiplication so that it uses a one-dimensional array for the matrix.
# pragma omp parallel for num_thread(thread_count) /
default(none) private(i, j) shared(A, x, y, m, n)
for (i = 0; i < m; i++) {
y[i] = 0.0;
for (j = 0; j < n; j++)
//y[i] += A[i][j] * x[j];
y[i] += A[i * n + j] * x[j];
}
5.12. Download the source file omp mat vect rand split.c from the book’s web- site. Find a program that does cache profiling (e.g., Valgrind [49]) and compile the program according to the instructions in the cache profiler documentation. (For example, with Valgrind you will want a symbol table and full optimiza- tion. (With gcc use, gcc − g − O2 . . . ). Now run the program according to the instructions in the cache profiler documentation, using input k × (k · 10 6 ), (k · 10 3 ) × (k · 10 3 ), and (k · 10 6 ) × k. Choose k so large that the number of level 2 cache misses is of the order 10 6 for at least one of the input sets of data.
a. How many level 1 cache write-misses occur with each of the three inputs?
b. How many level 2 cache write-misses occur with each of the three inputs?
d. How many level 1 cache read-misses occur with each of the three inputs?
e. How many level 2 cache read-misses occur with each of the three inputs?
A ordem das matrizes são 8 x 8.000.000, 8.000 x 8.000 e 8.000.000 x 8. Os resultados obtidos usando o valgrind estão apresentados a seguir:
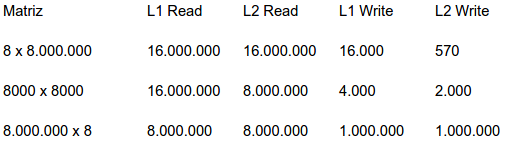
c. Where do most of the write-misses occur? For which input data does the program have the most write-misses? Can you explain why?
O maior numero de write-misses ocorre com a matriz de ordem 8.000.000 x 8. Neste sistema o array y tem ordem de 8.000.000, enquanto que nos outros sistemas sua ordem é de 8.000 e 8 respectivamente. Entre as variáveis A, x e y, y é a única variável que é escrita pelo código.
f. Where do most of the read-misses occur? For which input data does the program have the most read-misses? Can you explain why?
A maior quantidade de read-misses ocorre com a matriz de ordem 8 x 8.000.000. Cada elemento do array A vai ser lido uma única vez com os três inputs e, para cada input, A tem 64.000.000 de elementos. Os updates y[i] += … serão executados exatamente 64.000.000 de vezes e, como antes do loop interno ser executado y[i] é inicializado e provavelmente já está na cache, não causarão read-misses. As leituras de x[j] podem causar cache misses e no sistema de 8 x 8.000.000, x tem 8.000.000 de elementos, ao contrário dos outros dois sistemas com 8.000 e 8 elementos.
g. Run the program with each of the three inputs, but without using the cache profiler. With which input is the program the fastest? With which input is the program the slowest? Can your observations about cache misses help explain the differences? How?
Threads ---- 8 x 8.000.000 ---- 8.000 x 8.000 ---- 8.000.000 x 8
1 ---------- 0.43s ------------ 0.36s ------------ 0.42s
O programa mais lento é o com a matriz de ordem 8 x 8.000.000 e o mais rápido com a matriz de
ordem 8.000 x 8.000.
Read-misses tendem a ser mais custoso que write-misses.
Quando um programa necessita de dados para executar uma computação,
ele pode tanto tentar executar alguma outra computação ou esperar pelos dados.
Os dados criados por um write podem frequentemente ser enfileirados e a computação pode
prosseguir.
O programa com a matriz de ordem 8.000.000 x 8 tem muito mais
write-misses que o programa com a matriz de ordem 8.000 x 8.000.
A quantidade de L2 read-misses entre os dois programas é idêntica e a diferença
de L1 read-misses é muito menos custosa que L2 read-misses. Portanto o programa
com a matriz de ordem 8.000 x 8.000 é mais rápido.
5.13. Recall the matrix-vector multiplication example with the 8000 × 8000 input. Suppose that thread 0 and thread 2 are assigned to different processors. If a cache line contains 64 bytes or 8 double s, is it possible for false sharing between threads 0 and 2 to occur for any part of the vector y ? Why? What about if thread 0 and thread 3 are assigned to different processors; is it possible for false sharing to occur between them for any part of y ?
Com 8000 elementos y será particionando (aproximadamente) como segue:
Thread 0: y[0], y[1] , … , y[1999] Thread 1: y[2000], y[2001] , … , y[3999] Thread 2: y[4000], y[4001] , … , y[5999] Thread 3: y[6000], y[6001] , … , y[7999]
Para ocorrer falso-compartilhamento entre as threads 0 e 2, deve haver elementos de y que pertencem à mesma linha de cache, mas associadas à threads diferentes. Na thread 0, a linha de cache que está mais "próxima" dos elementos associados à thread 2 é a linha que contém y[1999]. Mas mesmo que este seja o primeiro elemento da linha de cache, o índice mais alto possível para um elemento de y que pertence a esta linha é 2006:
y[1999] y[2000] y[2001] y[2002] y[2003] y[2004] y[2005] y[2006]
Já que o menor index de um elemento de y associado à thread 2 é 4000, não existe a possibilidade de uma linha de cache ter elementos que pertencem tanto à thread 0 quanto à thread 2. Raciocínio similar se aplica às threads 0 e 3.
5.14. Recall the matrix-vector multiplication example with an 8 × 8, 000, 000 matrix. Suppose that double s use 8 bytes of memory and that a cache line is 64 bytes. Also suppose that our system consists of two dual-core processors.
Verificando a localização de y[0] na primeira linha de cache contendo todo ou parte de y, vemos que y pode ser distribuído entre as linhas de cache de 8 formas diferentes. Se y[0] é o primeiro elemento da linha de cache, então a distribuição de y na cache será:
1ª linha: y[0] y[1] y[2] y[3] y[4] y[5] y[6] y[7]
Se y[0] é o segundo elemento da linha de cache, então a distribuição será:
1ª linha: ---- y[0] y[1] y[2] y[3] y[4] y[5] y[6]
2ª linha: y[7] ---- ---- ---- ---- ---- ---- ----
Se y[0] é o último elemento da primeira linha, então a distribuição será:
1ª linha: ---- ---- ---- ---- ---- ---- ---- y[0]
2ª linha: y[1] y[2] y[3] y[4] y[5] y[6] y[7] ----
a. What is the minimum number of cache lines that are needed to store the vector y ?
Do primeiro exemplo vemos que é possível que y caiba em uma única linha de cache.
b. What is the maximum number of cache lines that are needed to store the vector y ?
No máximo ele ocupará duas linhas de cache.
c. If the boundaries of cache lines always coincide with the boundaries of 8-byte double s, in how many different ways can the components of y be assigned to cache lines?
Se os limites sempre coincidem, sempre haverá apenas uma possibilidade.
d. If we only consider which pairs of threads share a processor, in how many different ways can four threads be assigned to the processors in our computer? Here, we’re assuming that cores on the same processor share cache.
Podemos escolher 2 das threads e atribuí-las a um dos processadores: 0 e 1, 0 e 2, 0 e 3 ou 0 e 4. Então existem 4 atribuições possíveis das threads para os processadores.
e. Is there an assignment of components to cache lines and threads to proces- sors that will result in no false-sharing in our example? In other words, is it possible that the threads assigned to one processor will have their compo- nents of y in one cache line, and the threads assigned to the other processor will have their components in a different cache line?
Sim. Supondo que as threads 0 e 1 compartilham um processador e as threads 2 e 3 compartilham outro. Então se y[0], y[1], y[2] e y[3] estão em uma linha de cache e y[4], y[5], y[6] e y[7] estão em outra, qualquer escrita pela thread 0 ou 1 não irá invalidar a linha contendo os dados na linha de cache das threads 2 e 3. Da mesma forma, escritas por 2 e 3 não irão invalidar os dados na cache de 0 e 1.
f. How many assignments of components to cache lines and threads to processors are there?
Para cada uma das 4 atribuições de threads para processadores, existem 8 atribuições possíveis de y para linhas de cache. Portanto temos um total de 4 * 8 = 32 atribuições.
g. Of these assignments, how many will result in no false sharing?
Apenas uma possibilidade, aquela que é apresentada na letra e).
5.15.
5.16.