Programação Concorrente e Distribuída (4)
Esta página tem como objetivo apresentar a resolução dos exercícios do livro "An Introduction to Parallel Programming" de Peter Pacheco. A resolução dessas listas foi utilizada durante o curso de Programação Paralela no DCA / UFRN.
Respostas dos capítulos:
-
Chapter 04 - Shared-Memory Programming with Pthreads
Chapter 04 - Shared-Memory Programming with Pthreads
4.1. When we discussed matrix-vector multiplication we assumed that both m and n, the number of rows and the number of columns, respectively, were evenly divisible by t, the number of threads. How do the formulas for the assignments change if this is not the case?
Para que o cálculo também funcionasse para um número de linhas não divisível pelo número de threads (m % thread_count != 0), o resto dessa divisão foi distribuído entre as threads com my_rank menor que o resto. Além disso, as threads que não tiveram o resto distribuído, tiveram que fazer um deslocamento igual ao resto para compensar os local_m+1 das threads com resto distribuído. Código da função executada pelas threads e modificada do arquivo “pth_mat_vect.c” fornecido pelo livro texto está a seguir. O arquivo modificado pode ser baixado aqui.
/*------------------------------------------------------------------
* Function: Pth_mat_vect
* Purpose: Multiply an mxn matrix by an nx1 column vector
* In arg: rank
* Global in vars: A, x, m, n, thread_count
* Global out var: y
*/
void *Pth_mat_vect(void* rank) {
long my_rank = (long) rank;
int i, j;
int local_m = m/thread_count;
int my_first_row;
int my_last_row;
if(my_rank < (m % thread_count)){ //Se minha thread atual tem um
// my_rank menor que o resto da divisao de m pelo thread_count, então ela recebe o resto da divisão
local_m++;
my_first_row = my_rank*local_m;
my_last_row = (my_rank+1)*local_m - 1;
}else{ //Para as outras threads, adicionar o resto para compensar os local_m+1 das outras threads
my_first_row = my_rank*local_m + (m % thread_count);
my_last_row = (my_rank+1)*local_m - 1 + (m % thread_count);
}
for (i = my_first_row; i <= my_last_row; i++) {
y[i] = 0.0;
for (j = 0; j < n; j++)
y[i] += A[i*n+j]*x[j];
}
return NULL;
} /* Pth_mat_vect */
4.2. If we decide to physically divide a data structure among the threads, that is, if we decide to make various members local to individual threads, we need to consider at least three issues:
a. How are the members of the data structure used by the individual threads?
b. Where and how is the data structure initialized?
c. Where and how is the data structure used after its members are computed?
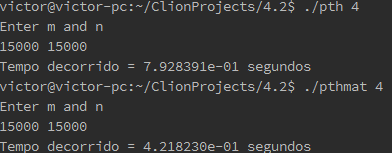
Para que as linhas da matriz A e os blocos de memória do vetor y fossem divididos, foi necessário criar um local_y e um local_A para cada thread. Quanto de memória é alocado para essas estruturas de dados, é definido no cálculo do local_m e local_n. São feitas as atribuições do A para o local_A de cada thread, então o cálculo só é realizado com os local_A e local_y. No final, o resultado das threads é lançado dos local_y para o y. Já em relação ao tempo de execução, essa estratégia foi mais demorada. Isso ocorre porque cada thread deve realizar uma copia dos seus local_y e local_A, fazendo com que haja uma perda de tempo ao realizar esse processo. No caso de utilizar uma variável global torna-se o processo mais rápido, pois além de não perder tempo copiando, há a possibilidade dos dados já estarem na cache. O código pode ser acesado por aqui.
/*------------------------------------------------------------------
* Function: Pth_mat_vect
* Purpose: Multiply an mxn matrix by an nx1 column vector
* In arg: rank
* Global in vars: A, x, m, n, thread_count
* Global out var: y
*/
void *Pth_mat_vect(void* rank) {
long my_rank = (long) rank;
int i, j;
int local_m = m/thread_count; //Divisão das linhas de A
int local_n = n/thread_count; //Divisão do vetor y
int my_first_row;
int my_last_row;
int my_first_column;
int my_last_column;
double* local_y; //Vetor produto local
double* local_A; //Matriz A local
//Distribuição das linhas da matriz A
if(my_rank < (m % thread_count)){ //Se minha thread atual
// tem um my_rank menor que o resto da divisao de m pelo thread_count,
// então ela recebe o resto da divisão
local_m++;
my_first_row = my_rank*local_m;
my_last_row = (my_rank+1)*local_m - 1;
}else{
//Para as outras threads, adicionar o resto para compensaros local_m+1 das outras threads
my_first_row = my_rank*local_m + (m % thread_count);
my_last_row = (my_rank+1)*local_m - 1 + (m % thread_count);
}
//Distribuição do vetor y
if(my_rank < (n % thread_count)){
//Se minha thread atual tem um my_rank menor que
// o resto da divisao de n pelo thread_count, então ela recebe o resto da divisão
local_n++;
my_first_column = my_rank*local_n;
my_last_column = (my_rank+1)*local_n - 1;
}else{ //Para as outras threads, adicionar o resto para compensar os local_m+1 das outras threads
my_first_column = my_rank*local_n + (n % thread_count);
my_last_column = (my_rank+1)*local_n - 1 + (n % thread_count);
}
//Aloca memória
local_A = malloc(local_m*n*sizeof(double));
local_y = malloc(local_n*sizeof(double));
//Realiza as atribuições do local_A
for(i=0;i<local_m;i++){
for (j = 0; j < n; j++){
local_A[i*n + j] = A[my_first_row*n+j];
}
my_first_row++;
}
//Realiza o cálculo local
for (i = 0; i < local_m; i++) {
local_y[i] = 0.0;
for (j = 0; j < local_n; j++)
local_y[i] += local_A[i*n+j]*x[j];
}
//Junta o resultado novamente
for (i = 0; i < local_n; i++) {
y[my_first_column] = local_y[i];
my_first_column++;
}
return NULL;
} /* Pth_mat_vect */
(Primeira execução é a nova implementação)
4.34.4. The performance of the \(\pi\) calculation program that uses mutexes remains roughly constant once we increase the number of threads beyond the number of available CPUs. What does this suggest about how the threads are scheduled on the available processors?
O tempo permanece constante pois as threads não vão estar executando em paralelo, mas sim, disputando para poderem ser executadas nas CPUs disponíveis. A melhor forma de escalonar essas tarefas seria distribuindo as threads igualmente para cada CPU e cada thread executaria em uma quantidade fixa de tempo, sem necessidade de determinar prioridade entre elas.
4.5. Modify the mutex version of the \(\pi\) calculation program so that the critical section is in the for loop. How does the performance of this version compare to the performance of the original busy-wait version? How might we explain this?
for (i = my_first_i; i < my_last_i; i++, factor = -factor) { pthread_mutex_lock(&mutex); sum += factor/(2*i+1); pthread_mutex_unlock(&mutex); }for (i = my_first_i; i < my_last_i; i++, factor = -factor) { while (flag != my_rank); sum += factor/(2*i+1); flag = (flag+1) % thread_count; }Busy:
Mutex:
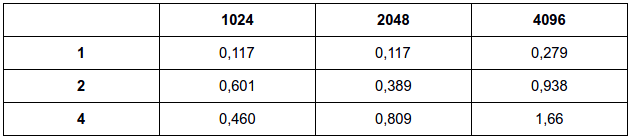
A performance é similar no mutex modificado, já que é feita uma operação de lock e unlock em cada iteração das thread para cálculo do \(\pi\). Como a espera ocupada é bastante baixa, não há muito prejuízo em comparação ao mutex, que coloca a thread para o estado de espera.
4.6. Modify the mutex version of the calculation program so that it uses a semaphore instead of a mutex. How does the performance of this version compare with the mutex version?
Semáforo:
for (i = my_first_i; i < my_last_i; i++, factor = -factor) { sem_wait(&mutex); sum += factor/(2*i+1); sem_post(&mutex); }Mutex:
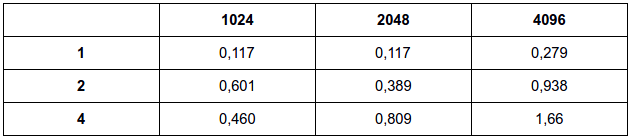
Semáforo:
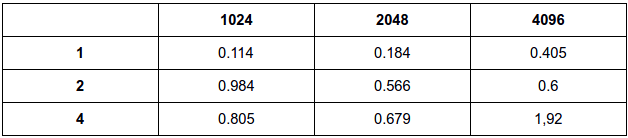
A implementação com semáfoto obteve resultados parecidos com a implementação em mutex. Como somente uma thread pode executar a funcionalidade por vez, o desempenho torna-se parecido com o desempenho do mutex.
4.7. Although producer-consumer synchronization is easy to implement with semaphores, it’s also possible to implement it with mutexes. The basic idea is to have the producer and the consumer share a mutex. A flag variable that’s initialized to false by the main thread indicates whether there’s anything to consume. With two threads we’d execute something like this:
while (1) { pthread_mutex_lock(&mutex); if (my rank == consumer) { if (message available) { print message; pthread_mutex_unlock(&mutex); break; } } else { // my rank == producer create message; message available = 1; pthread_mutex_unlock(&mutex); break; } pthread_mutex_unlock(&mutex); }So if the consumer gets into the loop first, it will see there’s no message available and return to the call to pthread_mutex_lock. It will continue this process until the producer creates the message. Write a Pthreads program that implements this version of producer-consumer synchronization with two threads. Can you generalize this so that it works with 2k threads–odd-ranked threads are consumers and even-ranked threads are producers? Can you generalize this so that each thread is both a producer and a consumer? For example, suppose that thread q “sends” a message to thread (q+1) mod t and “receives” a message from thread (q-1+t) mod t? Does this use busy-waiting?
Código Implementado 1
Código Implementado 2
Código Implementado 3
Para a solução com duas threads, o código está a seguir:
/*-------------------------------------------------------------------*/ void *Hello(void* rank) { long my_rank = (long) rank; /* Use long in case of 64-bit system */ while (1) { pthread_mutex_lock(&mutex); if (my_rank == consumer) { if (message_avaliable) { printf("Consumidor imprimiu mensagem\n"); pthread_mutex_unlock(&mutex); break; } } else { /* my rank == producer */ printf("Produtor criou mensagem\n"); message_avaliable = 1; pthread_mutex_unlock(&mutex); break; } pthread_mutex_unlock(&mutex); } return NULL; } /* Hello */
Para a solução com threads ímpares sendo consumidoras e pares sendo produtoras, o código está a seguir:
void *Hello(void* rank) { long my_rank = (long) rank; /* Use long in case of 64-bit system */ while (1) { pthread_mutex_lock(&mutex); if (my_rank % 2 != 0) { //Consumidor é ímpar if (message_avaliable) { printf("Consumidor %li imprimiu mensagem\n",my_rank); message_avaliable = 0; pthread_mutex_unlock(&mutex); break; } } else { //Produtor é par printf("Produtor %li criou mensagem\n",my_rank); message_avaliable = 1; pthread_mutex_unlock(&mutex); break; } pthread_mutex_unlock(&mutex); } return NULL; } /* Hello */
Para a solução em que qualquer thread pode ser consumidora ou produtora está a seguir:
void *Hello(void* rank) { long my_rank = (long) rank; /* Use long in case of 64-bit system */ while (1) { pthread_mutex_lock(&mutex); if(message_avaliable == 0){ printf("Produtor %li criou mensagem\n",my_rank); message_avaliable = 1; pthread_mutex_unlock(&mutex); break; }else{ printf("Consumidor %li imprimiu mensagem\n",my_rank); message_avaliable = 0; pthread_mutex_unlock(&mutex); break; } } return NULL; } /* Hello */
Se a solução usasse o modo de envio das mensagens de uma thread “q” para uma “q+1”, as threads que não conseguiram o lock deverão esperar até que todas as outras anteriores enviem e recebam suas mensagens para que possam enviar as suas.
4.8. If a program uses more than one mutex, and the mutexes can be acquired in different orders, the program can deadlock. That is, threads may block forever waiting to acquire one of the mutexes. As an example, suppose that a program has two shared data structures–for example, two arrays or two linked lists–each of which has an associated mutex. Further suppose that each data structure can be accessed (read or modified) after acquiring the data structure’s associated mutex.
a. Suppose the program is run with two threads. Further suppose that the following sequence of events occurs:
What happens?
Ocorre deadlock. Isso ocorre porque no tempo 0, a Thread 0 faz um lock no mut0 e a Thread 1 faz um lock no mut1. No tempo 1, a Thread 0 tenta dar um lock no mut1, mas ele já foi adquirido pela Thread 1, então ela fica “presa”. Já a Thread 1, tenta dar um lock no mut0, mas ele já foi adquirido pela Thread 0, então ela fica “presa”.
b. Would this be a problem if the program used busy-waiting (with two flag variables) instead of mutexes?
Também ocorreria o mesmo problema, já que o busy-waiting utiliza o mesmo princípio do mutex.
c. Would this be a problem if the program used semaphores instead of mutexes?
Não ocorreria problema se usássemos um semáforo com contador igual a 2. Isso ocorre porque essa estrutura não permite que ocorra deadlock, já que quando uma seção crítica está bloqueada, a outra tem que estar liberada.
4.9. Some implementations of Pthreads define barriers. The function
initializes a barrier object, barrier_p. As usual, we’ll ignore the second argument and just pass in NULL. The last argument indicates the number of threads that must reach the barrier before they can continue. The barrier itself is a call to the function
As with most other Pthreads objects, there is a destroy function
Modify one of the barrier programs from the book’s website so that it uses a Pthreads barrier. Find a system with a Pthreads implementation that includes barrier and run your program with various numbers of threads. How does its performance compare to the other implementations?
Código Implementado 1
Código Implementado 2
Código com pthread_barrier:
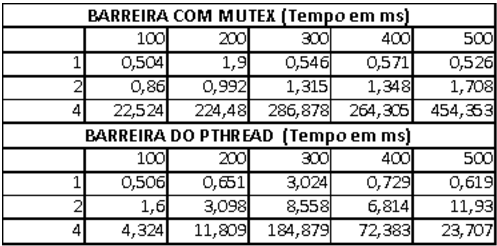
for (i = 0; i < BARRIER_COUNT; i++) { barrier_thread_counts[i]++; pthread_barrier_wait(&barrier_p); }Código com mutex:
for (i = 0; i < BARRIER_COUNT; i++) { pthread_mutex_lock(&barrier_mutex); barrier_thread_counts[i]++; pthread_mutex_unlock(&barrier_mutex); while (barrier_thread_counts[i] < thread_count); }A performance usando barreira foi melhor do que a estratégia de simular barreira com busy waiting, já que a implementação usa busy-waiting e a de barreira já é uma função otimizada do pthread, aumentando o desempenho. Na tabela abaixo, o número de barreiras foi crescendo junto com o número de threads.
4.10. Modify one of the programs you wrote in the Programming Assignments that follow so that it uses the scheme outlined in Section 4.8 to time itself. In order to get the time that has elapsed since some point in the past, you can use the macro GET_TIME defined in the header file timer.h on the book’s website. Note that this will give wall clock time, not CPU time. Also note that since it’s a macro, it can operate directly on its argument. For example, to implement
Store current time in my start;
you would use
GET_TIME(my_start);notGET_TIME(&my_start);How will you implement the barrier? How will you implement the following pseudo code?
elapsed = Maximum of my_elapsed values;Foi escolhido o exercício de programação 4.4. Ele pede para medir o tempo médio que o sistema leva para criar e terminar uma thread. Aqui esse problema foi adaptado e foi colocado para ele calcular o tempo de execução de um laço for em cada thread. Implementou-se uma barreira utilizando o “pthread_barrier_t” para sincronizar as threads e ver qual era o maior tempo de execução. Para calcular o tempo máximo, criou-se a variável global “elapsed”. Cada thread calculava seu tempo e comparava com o armazenado nessa variável. Se o tempo fosse maior, o valor de “elapsed” era substituído. Com isso, temos o tempo desejado. Código está a seguir, junto com exemplo de execução do programa:
void* Thread_function(void* rank) { long my_rank = (long) rank; double my_start, my_finish, my_elapsed; pthread_barrier_wait(&barrier_p); int i; GET_TIME(my_start); for (i = 0; i < 100000; i++); GET_TIME(my_finish); my_elapsed = my_finish - my_start; pthread_mutex_lock(&mutex); if(my_elapsed > elapsed){ elapsed = my_elapsed; } pthread_mutex_unlock(&mutex); return NULL; } /* Thread_function */
4.11.Give an example of a linked list and a sequence of memory accesses to the linked list in which the following pairs of operations can potentially result in problems:
a. Two deletes executed simultaneously
Um problema de dois deletes simultâneos pode ocorrer por exemplo se há a tentativa de apagar dois elementos sucessivos da lista. Nessa situação um dos elementos não irá apontar o antecessor do elemento seguinte para o elemento que estaria sendo apagado pela outra thread.
b. An insert and a delete executed simultaneously
Um elemento estaria sendo inserido numa posição antecessora ou sucessora ao elemento que estaria sendo apagado por outra thread. Nessa situação, o elemento que estaria sendo inserido poderia apontar para o elemento que foi apagado pela outra thread.
c. A member and a delete executed simultaneously
Um elemento foi encontrado sendo que ele tinha sido deletado da lista por outra thread.
d. Two inserts executed simultaneously
Dois elementos sendo inseridos na mesma posição da lista, por duas threads. Nessa situação, cada um dos elementos estaria apontando para a referência do elemento sucessor e um deles não estaria “visível” na lista no final do procesos.
e. An insert and a member executed simultaneously
Um elemento foi inserido na lista no entanto, a outra thread mantinha a referência antiga do elemento que precedia o elemento inserido e portanto não encontrou o elemento no método member.
4.12.The linked list operations Insert and Delete consist of two distinct “phases.” In the first phase, both operations search the list for either the position of the new node or the position of the node to be deleted. If the outcome of the first phase so indicates, in the second phase a new node is inserted or an existing node is deleted. In fact, it’s quite common for linked list programs to split each of these operations into two function calls. For both operations, the first phase involves only read-access to the list; only the second phase modifies the list. Would it be safe to lock the list using a read-lock for the first phase? And then to lock the list using a write-lock for the second phase? Explain your answer.
Seria sim, já que essas duas regiões de procura e ação sobre o valor são críticas. Assim, como um lock de read-write poderia remover o problema com o problema de concorrência na hora de deletar ou inserir um valor.
4.13 Download the various threaded linked list programs from the website. In our examples, we ran a fixed percentage of searches and split the remaining percentage among inserts and deletes.
a. Rerun the experiments with all searches and all inserts.
b. Rerun the experiments with all searches and all deletes. Is there a difference in the overall run-times? Is insert or delete more expensive?
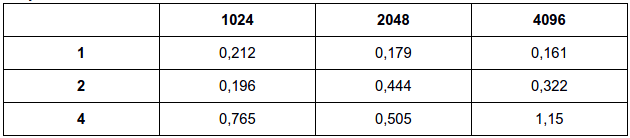
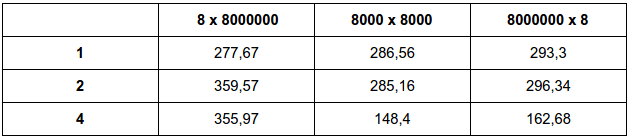
Executando com 50% de search e 50% de insert para 1000 initial keys e 100000 operações. Valores em segundos. Não foi executados para 8 Threads pois a máquina só possuia 4 núcleos.
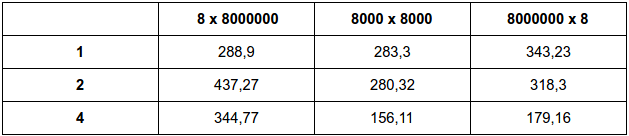
Executando com 50% de search e 50% de delete para 1000 initial keys e 100000 operações. Valores em segundos. Não foi executados para 8 Threads pois a máquina só possuia 4 núcleos.
Executando para somente uma thread já é possível a grande diferença nos tempos de execução entre o Insert e o Delete. Assim como nos exemplos do livro, a implementação por read-write e one mutex for Entire List obtiveram melhores resultados em ambos os casos. Além disso, enquanto as operações com insert resultaram em valores na casa dos segundos por delete resultou na casa de milissegundos, sendo este último mais rápido e menos custoso.
4.14. Recall that in C a function that takes a two-dimensional array argument must specify the number of columns in the argument list. Thus it is quite common for C programmers to only use one-dimensional arrays, and to write explicit code for converting pairs of subscripts into a single dimension. Modify the Pthreads matrix-vector multiplication so that it uses a one-dimensional array for the matrix and calls a matrix-vector multiplication function. How does this change affect the run-time?
Correção: A implementação original já é realizada com um array de uma dimensão. O que foi feito foi substituir a implementação de uma dimensão por uma de 2 dimensões
Original (array de uma dimensão):
Implementação (matriz com linhas e colunas):
Como já era esperado, a implementação do array com uma dimensão em comparação com a matriz de linhas e colunas não afeta o desempenho.
4.15. Download the source file pth mat vect rand split.c from the book’s web-site. Find a program that does cache profiling (for example, Valgrind [49]) and compile the program according to the instructions in the cache profiler documentation. (with Valgrind you will want a symbol table and full optimization gcc − g − O2 . . . ). Now run the program according to the instructions in the cache profiler documentation, using input k × (k · 10⁶ ), (k · 10³ ) × (k · 10³ ), and (k · 10⁶ ) × k. Choose k so large that the number of level 2 cache misses is of the order 10⁶ for at least one of the input sets of data.
Segundo a documentação do Valgrind Cachegrind:

Assim, como o programa foi executado em uma máquina com até cache L3, as caches L2 e L3 foram “simuladas” dentro da last level cache (LL)
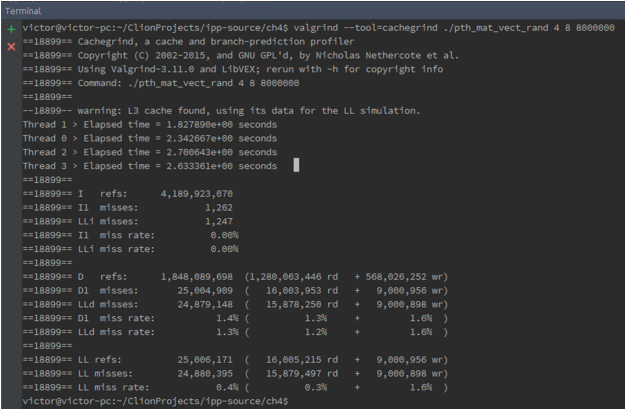
Para 8 x 8000000
Para 8000 x 8000

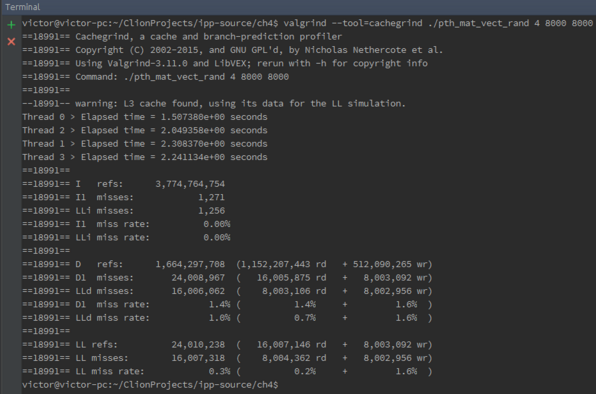
Para 8000000 x 8:
a. How many level 1 cache write-misses occur with each of the three inputs?
Para 8 x 8000000: 9.000.956 misses de escrita
Para 8000 x 8000: 8.003.092 misses de escrita
Para 8000000 x 8: 9.000.983 misses de escritab. How many level 2 cache write-misses occur with each of the three inputs?
Para 8 x 8000000: 9.000.898 misses de escrita (na cache de mais auto nivel L3)
Para 8000 x 8000: 8.002.956 misses de escrita
Para 8000000 x 8: 9.000.904 misses de escritac. Where do most of the write-misses occur? For which input data does the program have the most write-misses? Can you explain why?
Os misses de write ocorreram mais na cache de nível 1 do que na do nível 2, o que já seria esperado, pois havendo miss na cache de nível 1, não necessariamente ocorrerá miss na cache de nível 2. O programa teve maiores quantidades de miss para as entradas de 8 x 8000000 e 8000000 x 8. Para a primeira entrada, Uma linha da matriz contém 8 milhões de entrada, assim como o tamanho do vetor x. Portanto, nessa situação, muito provavelmente a cache da cpu não conseguirá armazenar todo o tamanho do vetor x nem de toda a linha da matriz, tendo portanto que realizar vários acessos a memória principal afim de obter os valores. Já no segundo tipo de entrada, uma única linha da matriz contém apenas 8 valores, sendo que a cache irá buscar os outros elementos seguintes da matriz afim de preencher toda a linha de cache. Assim, as caches de cada CPU poderão ter referências para elementos que outras threads estão acessando. Quando uma outra thread modifica um elemento na sua cache, toda a linha da cache fica “dirty”, fazendo com que as caches tenham que acessar novamente a memória principal para obter os valores atualizados dos elementos, isso é chamado de false sharing. Além disso, ocorre o problema em que cada núcleos das threads perdem tempo ao ter que buscar mais elementos do que os 8 que cada thread precisa, afim de preencher a linha da cache.
d. How many level 1 cache read-misses occur with each of the three inputs?
Para 8 x 8000000: 16.003.593 misses de leitura
Para 8000 x 8000: 16.005.875 misses de leitura
Para 8000000 x 8: 8.003.603 misses de leiturae. How many level 2 cache read-misses occur with each of the three inputs?
Para 8 x 8000000: 15.878.250 misses de leitura
Para 8000 x 8000: 8.003.106 misses de leitura
Para 8000000 x 8: 8.002.949 misses de leituraf. Where do most of the read-misses occur? For which input data does the program have the most read-misses? Can you explain why?
A maior parte dos cache miss de leitura ocorreram no nível 1 como já era esperado e foi justificado na letra c. O programa teve um maior read miss para 8 x 8000000, olhando a cache nível 2, que foi a que efetivamente fez com que fosse acessado diretamente a memória principal.
g. Run the program with each of the three inputs, but without using the cache profiler. With which input is the program the fastest? With which input is the program the slowest? Can your observations about cache misses help explain the differences? How?
Para 8 x 8000000

Para 8000 x 8000

Para 8000000 x 8
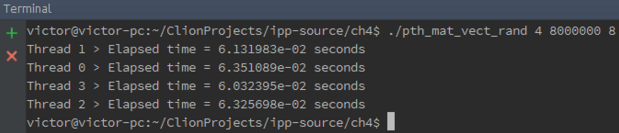
A entrada mais rápida foi a entrada 8000 x 8000 e a mais lenta foi a 8 x 8000000. Sim, as conclusões retiradas da análise feito por cache ajuda sim a entender o tempo de execução obtido, pois como as entradas de 8 x 8000000 e 8000000 x 8 tiveram muito problemas com cache miss é esperado que elas obtenham um tempo de execução bem maior em comparação com a da entrada de 8000 x 8000.
4.16. Recall the matrix-vector multiplication example with the 8000 × 8000 input. Suppose that the program is run with four threads, and thread 0 and thread 2 are assigned to different processors. If a cache line contains 64 bytes or eight doubles, is it possible for false sharing between threads 0 and 2 to occur for any part of the vector y ? Why? What about if thread 0 and thread 3 are assigned to different processors–is it possible for false sharing to occur between them for any part of y ?
Com 8000 elementos y será particionando (aproximadamente) como segue:
Thread 0: y[0], y[1] , … , y[1999]
Thread 1: y[2000], y[2001] , … , y[3999]
Thread 2: y[4000], y[4001] , … , y[5999]
Thread 3: y[6000], y[6001] , … , y[7999]Para ocorrer falso-compartilhamento entre as threads 0 e 2, deve haver elementos de y que pertencem à mesma linha de cache, mas associadas à threads diferentes. Na thread 0, a linha de cache que está mais "próxima" dos elementos associados à thread 2 é a linha que contém y[1999]. Mas mesmo que este seja o primeiro elemento da linha de cache, o índice mais alto possível para um elemento de y que pertence a esta linha é 2006:
y[1999] y[2000] y[2001] y[2002] y[2003] y[2004] y[2005] y[2006]Já que o menor index de um elemento de y associado à thread 2 é 4000, não existe a possibilidade de uma linha de cache ter elementos que pertencem tanto à thread 0 quanto à thread 2. Raciocínio similar se aplica às threads 0 e 3.
4.17. Recall the matrix-vector multiplication example with an 8 × 8, 000, 000 matrix. Suppose that double s use 8 bytes of memory and that a cache line is 64 bytes. Also suppose that our system consists of two dual-core processors.
Verificando a localização de y[0] na primeira linha de cache contendo todo ou parte de y, vemos que y pode ser distribuído entre as linhas de cache de 8 formas diferentes. Se y[0] é o primeiro elemento da linha de cache, então a distribuição de y na cache será:
1ª linha:
y[0] y\[1] y[2] y[3] y[4] y[5] y[6] y[7]Se y[0] é o segundo elemento da linha de cache, então a distribuição será:
1ª linha:
---- y[0] y\[1] y[2] y[3] y[4] y[5] y[6]
2ª linha:y[7] ---- ---- ---- ---- ---- ---- ----Se y[0] é o último elemento da primeira linha, então a distribuição será:
1ª linha:
---- ---- ---- ---- ---- ---- ---- y[0]
2ª linha:y\[1] y[2] y[3] y[4] y[5] y[6] y[7] ----a. What is the minimum number of cache lines that are needed to store the vector y ?
Do primeiro exemplo vemos que é possível que y caiba em uma única linha de cache.
b. What is the maximum number of cache lines that are needed to store the vector y ?
No máximo ele ocupará duas linhas de cache.
c. If the boundaries of cache lines always coincide with the boundaries of 8-byte double s, in how many different ways can the components of y be assigned to cache lines?
Se os limites sempre coincidem, sempre haverá apenas uma possibilidade.
d. If we only consider which pairs of threads share a processor, in how many different ways can four threads be assigned to the processors in our computer? Here, we’re assuming that cores on the same processor share cache.
Podemos escolher 2 das threads e atribuí-las a um dos processadores: 0 e 1, 0 e 2, 0 e 3 ou 0 e 4. Então existem 4 atribuições possíveis das threads para os processadores.
e. Is there an assignment of components to cache lines and threads to processors that will result in no false-sharing in our example? In other words, is it possible that the threads assigned to one processor will have their components of y in one cache line, and the threads assigned to the other processor will have their components in a different cache line?
Sim. Supondo que as threads 0 e 1 compartilham um processador e as threads 2 e 3 compartilham outro. Então se y[0], y[1], y[2] e y[3] estão em uma linha de cache e y[4], y[5], y[6] e y[7] estão em outra, qualquer escrita pela thread 0 ou 1 não irá invalidar a linha contendo os dados na linha de cache das threads 2 e 3. Da mesma forma, escritas por 2 e 3 não irão invalidar os dados na cache de 0 e 1.
f. How many assignments of components to cache lines and threads to processors are there?
Para cada uma das 4 atribuições de threads para processadores, existem 8 atribuições possíveis de y para linhas de cache. Portanto temos um total de 4 * 8 = 32 atribuições.
g. Of these assignments, how many will result in no false sharing?
Apenas uma possibilidade, aquela que é apresentada na letra e).
4.18.
a. Modify the matrix-vector multiplication program so that it pads the vector y when there’s a possibility of false sharing. The padding should be done so that if the threads execute in lock-step, there’s no possibility that a single cache line containing an element of y will be shared by two or more threads. Suppose, for example, that a cache line stores eight doubles and we run the program with four threads. If we allocate storage for at least 48 doubles in y , then, on each pass through the for i loop, there’s no possibility that two threads will simultaneously access the same cache line.
Correção: Não seriam necessários no mínimo 48 doubles, mas sim 32 doubles. Por exemplo, caso m = 8 e o programa fosse executado para 4 threads então seriam necessários pelo menos 32 doubles para se garantir nenhum false sharing (cada thread estaria responsável por 2 elementos os outros 6 seriam preenchidos (“pads”), logo (2 + 6) * 4 = 32). O preenchimento seria realizado somente para m < 32. A modificação então fica:
Código Implementado 1
Código Implementado 2
Código Implementado 3
int SIZE_DOUBLE = 8; if (m < SIZE_DOUBLE*thread_count) { y = malloc(SIZE_DOUBLE*thread_count* sizeof(double)); } else { y = malloc(m*sizeof(double)); }*local_m = m/thread_count; if (m < SIZE_DOUBLE*thread_count) { *my_first_row = my_rank*SIZE_DOUBLE; *my_last_row = SIZE_DOUBLE*my_rank + *local_m; } else { *my_first_row = my_rank*(*local_m); *my_last_row = *my_first_row + *local_m; }b. Modify the matrix-vector multiplication so that each thread uses private storage for its part of y during the for i loop. When a thread is done computing its part of y , it should copy its private storage into the shared variable.
double * y_aux = malloc(m*sizeof(double)); GET_TIME(start); for (i = my_first_row; i < my_last_row; i++) { y_aux[i] = 0.0; for (j = 0; j < n; j++) { temp = A[sub++]; temp *= x[j]; y_aux[i] += temp; } } copiaVetor(y_aux, y, my_first_row, my_last_row); GET_TIME(finish);c. How does the performance of these two alternatives compare to the original program? How do they compare to each other?
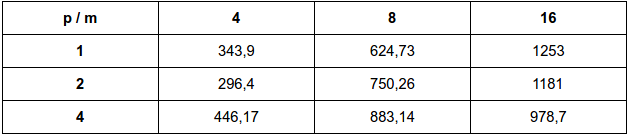
Fazendo para m = 4, 8 e 16 e n = 20.000.000
Resultados em milissegundos
Original:
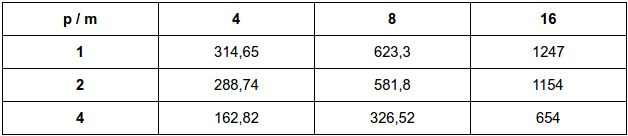
a:
b:
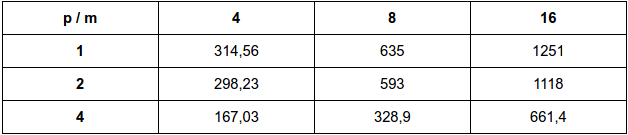
O desempenho em relação a implementação original foi significativa principalmente quando se analisa com um maior número de threads. Em relação ao desempenho entre as duas formas de implementação, nota-se que são bastante equivalentes, diferenciando em poucos milisegundos, o que dificulta afirmar qual tipo de implementação seria melhor.
4.19.Gostou desta página? Compartilhe ou deixe um comentário abaixo!
comments powered by Disqus